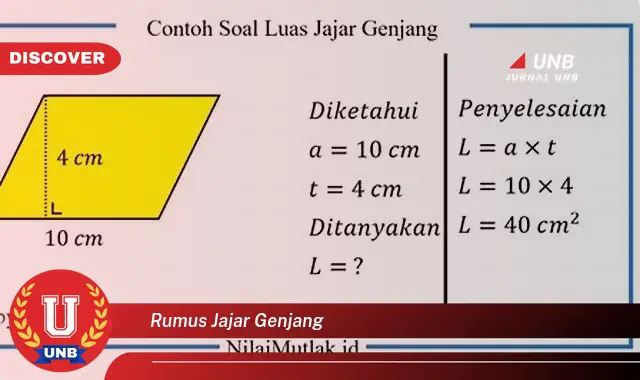
Rumus jajar genjang adalah suatu rumus yang digunakan untuk menghitung luas dan keliling jajar genjang. Rumus luas jajar genjang adalah L = a x t, dimana a adalah panjang alas dan t adalah tinggi jajar genjang. Sedangkan rumus keliling jajar genjang adalah K = 2(a + t), dimana a adalah panjang alas dan t adalah tinggi jajar genjang.
Rumus jajar genjang sangat penting dalam matematika, karena dapat digunakan untuk menyelesaikan berbagai masalah yang berkaitan dengan bangun datar jajar genjang. Misalnya, rumus tersebut dapat digunakan untuk menghitung luas tanah yang berbentuk jajar genjang, atau untuk menghitung panjang pagar yang mengelilingi taman yang berbentuk jajar genjang.
Rumus jajar genjang telah dikenal sejak zaman dahulu. Ahli matematika Yunani, Euclid, menulis tentang rumus jajar genjang dalam bukunya “Elements” yang ditulis sekitar 300 SM. Rumus tersebut kemudian dikembangkan lebih lanjut oleh matematikawan India dan Persia pada abad pertengahan.
Rumus Jajar Genjang
Rumus jajar genjang merupakan konsep penting dalam matematika yang digunakan untuk menghitung luas dan keliling bangun datar jajar genjang. Berikut adalah tujuh aspek penting yang terkait dengan rumus jajar genjang:
- Luas
- Keliling
- Alas
- Tinggi
- Diagonal
- Sudut
- Kongruen
Luas jajar genjang dihitung menggunakan rumus L = a x t, di mana a adalah panjang alas dan t adalah tinggi jajar genjang. Keliling jajar genjang dihitung menggunakan rumus K = 2(a + t), di mana a adalah panjang alas dan t adalah tinggi jajar genjang. Diagonal jajar genjang membagi jajar genjang menjadi dua segitiga siku-siku yang kongruen. Sudut-sudut jajar genjang berhadapan sama besar.
Luas
Luas bangun datar merupakan ukuran yang menyatakan seberapa besar permukaan suatu bangun. Untuk menghitung luas jajar genjang, kita dapat menggunakan rumus L = a x t, dimana a adalah panjang alas dan t adalah tinggi jajar genjang. Luas jajar genjang memiliki beberapa sifat penting, di antaranya:
- Luas jajar genjang berbanding lurus dengan panjang alas dan tinggi jajar genjang.
- Luas jajar genjang tidak dipengaruhi oleh besar sudut-sudut jajar genjang.
- Jika dua jajar genjang memiliki alas dan tinggi yang sama, maka kedua jajar genjang tersebut memiliki luas yang sama.
Dalam kehidupan nyata, rumus luas jajar genjang sering digunakan untuk menghitung luas berbagai macam bangun datar, seperti luas tanah, luas lantai, dan luas kain. Pemahaman tentang luas jajar genjang sangat penting untuk menyelesaikan berbagai masalah matematika dan juga untuk aplikasi praktis dalam kehidupan sehari-hari.
Keliling
Keliling suatu bangun datar adalah panjang seluruh sisi bangun datar tersebut. Keliling jajar genjang dapat dihitung menggunakan rumus K = 2(a + t), dimana a adalah panjang alas dan t adalah tinggi jajar genjang. Keliling jajar genjang memiliki beberapa sifat penting, di antaranya:
- Keliling jajar genjang berbanding lurus dengan panjang alas dan tinggi jajar genjang.
- Keliling jajar genjang tidak dipengaruhi oleh besar sudut-sudut jajar genjang.
- Jika dua jajar genjang memiliki alas dan tinggi yang sama, maka kedua jajar genjang tersebut memiliki keliling yang sama.
Dalam kehidupan nyata, rumus keliling jajar genjang sering digunakan untuk menghitung keliling berbagai macam bangun datar, seperti keliling tanah, keliling pagar, dan keliling kain. Pemahaman tentang keliling jajar genjang sangat penting untuk menyelesaikan berbagai masalah matematika dan juga untuk aplikasi praktis dalam kehidupan sehari-hari.
Alas
Dalam rumus jajar genjang, alas merupakan salah satu besaran yang sangat penting. Alas jajar genjang adalah sisi sejajar yang dijadikan sebagai acuan untuk menghitung luas dan keliling jajar genjang.
-
Panjang Alas Berpengaruh Terhadap Luas Jajar Genjang
Luas jajar genjang berbanding lurus dengan panjang alasnya. Artinya, semakin panjang alas jajar genjang, maka semakin besar luas jajar genjang tersebut.
-
Panjang Alas Berpengaruh Terhadap Keliling Jajar Genjang
Keliling jajar genjang juga berbanding lurus dengan panjang alasnya. Artinya, semakin panjang alas jajar genjang, maka semakin besar keliling jajar genjang tersebut.
-
Panjang Alas dan Tinggi Berpengaruh Terhadap Luas Jajar Genjang
Luas jajar genjang dipengaruhi oleh panjang alas dan tinggi jajar genjang. Kedua besaran ini saling berinteraksi untuk menentukan luas jajar genjang.
-
Panjang Alas dan Tinggi Berpengaruh Terhadap Keliling Jajar Genjang
Keliling jajar genjang juga dipengaruhi oleh panjang alas dan tinggi jajar genjang. Namun, pengaruh kedua besaran ini berbeda dengan pengaruhnya terhadap luas jajar genjang.
Memahami hubungan antara alas dan rumus jajar genjang sangat penting untuk dapat menghitung luas dan keliling jajar genjang dengan benar. Selain itu, pemahaman ini juga dapat membantu kita dalam menyelesaikan masalah-masalah yang berkaitan dengan jajar genjang.
Tinggi
Tinggi merupakan salah satu besaran penting dalam rumus jajar genjang karena berpengaruh terhadap luas dan keliling jajar genjang. Tinggi jajar genjang adalah jarak tegak lurus antara alas dan sisi lainnya yang sejajar dengan alas.
Tinggi mempengaruhi luas jajar genjang secara langsung. Semakin tinggi jajar genjang, maka semakin besar pula luasnya. Hal ini disebabkan karena tinggi jajar genjang mempengaruhi jumlah satuan luas yang dapat ditampung oleh jajar genjang tersebut.
Selain itu, tinggi juga mempengaruhi keliling jajar genjang. Namun, pengaruhnya tidak sebesar pengaruh terhadap luas. Keliling jajar genjang dipengaruhi oleh panjang alas dan tinggi jajar genjang. Semakin tinggi jajar genjang, maka semakin besar kelilingnya. Namun, perubahan keliling tidak sebesar perubahan luas ketika tinggi jajar genjang berubah.
Memahami hubungan antara tinggi dan rumus jajar genjang sangat penting untuk dapat menghitung luas dan keliling jajar genjang dengan benar. Selain itu, pemahaman ini juga dapat membantu kita dalam menyelesaikan masalah-masalah yang berkaitan dengan jajar genjang.
Diagonal
Diagonal jajar genjang merupakan ruas garis yang menghubungkan dua titik sudut yang berlawanan pada jajar genjang. Diagonal jajar genjang memiliki sifat-sifat penting yang berkaitan dengan rumus jajar genjang.
Salah satu sifat penting diagonal jajar genjang adalah membagi jajar genjang menjadi dua segitiga siku-siku yang kongruen. Artinya, kedua segitiga tersebut memiliki luas yang sama. Sifat ini dapat digunakan untuk membuktikan rumus luas jajar genjang, yaitu dengan menjumlahkan luas kedua segitiga tersebut.
Selain itu, diagonal jajar genjang juga dapat digunakan untuk menentukan keliling jajar genjang. Panjang diagonal jajar genjang dapat dicari menggunakan teorema Pythagoras, yaitu dengan menghitung panjang sisi miring dari segitiga siku-siku yang terbentuk oleh diagonal dan setengah alas jajar genjang. Dengan mengetahui panjang diagonal, maka keliling jajar genjang dapat dihitung dengan menjumlahkan panjang keempat sisinya.
Memahami hubungan antara diagonal dan rumus jajar genjang sangat penting untuk dapat menghitung luas dan keliling jajar genjang dengan benar. Selain itu, pemahaman ini juga dapat membantu kita dalam menyelesaikan masalah-masalah yang berkaitan dengan jajar genjang.
Sudut
Sudut merupakan besaran penting dalam geometri, termasuk dalam rumus jajar genjang. Dalam jajar genjang, terdapat empat sudut yang besarnya sama, yaitu 90 derajat. Sudut-sudut ini memainkan peran penting dalam menentukan sifat-sifat dan rumus jajar genjang.
-
Besar Sudut mempengaruhi Luas Jajar Genjang
Besar sudut jajar genjang tidak berpengaruh terhadap luas jajar genjang. Luas jajar genjang hanya dipengaruhi oleh panjang alas dan tinggi jajar genjang.
-
Besar Sudut mempengaruhi Keliling Jajar Genjang
Besar sudut jajar genjang juga tidak berpengaruh terhadap keliling jajar genjang. Keliling jajar genjang hanya dipengaruhi oleh panjang alas dan tinggi jajar genjang.
-
Jenis Sudut Berpengaruh pada Bentuk Jajar Genjang
Jenis sudut jajar genjang menentukan bentuk jajar genjang. Jika keempat sudutnya siku-siku, maka jajar genjang tersebut berbentuk persegi panjang. Jika keempat sudutnya tidak siku-siku, maka jajar genjang tersebut berbentuk jajar genjang biasa.
-
Hubungan Sudut dengan Diagonal Jajar Genjang
Diagonal jajar genjang membagi jajar genjang menjadi dua segitiga siku-siku yang kongruen. Besar sudut-sudut segitiga siku-siku tersebut ditentukan oleh besar sudut jajar genjang.
Memahami hubungan antara sudut dan rumus jajar genjang sangat penting untuk dapat menghitung luas dan keliling jajar genjang dengan benar. Selain itu, pemahaman ini juga dapat membantu kita dalam menyelesaikan masalah-masalah yang berkaitan dengan jajar genjang.
Kongruen
Dalam matematika, kongruen mengacu pada dua bangun datar atau bangun ruang yang memiliki bentuk dan ukuran yang sama. Dalam rumus jajar genjang, konsep kongruen berkaitan dengan sifat diagonal jajar genjang yang membagi jajar genjang menjadi dua segitiga siku-siku yang kongruen.
Kongruennya kedua segitiga siku-siku tersebut memberikan implikasi penting dalam menghitung luas jajar genjang. Karena kedua segitiga tersebut memiliki luas yang sama, maka luas jajar genjang dapat dihitung dengan menjumlahkan luas kedua segitiga tersebut. Hal ini menjadi dasar dari rumus luas jajar genjang, yaitu L = a x t, di mana a adalah panjang alas dan t adalah tinggi jajar genjang.
Selain itu, sifat kongruen diagonal jajar genjang juga memudahkan dalam menghitung keliling jajar genjang. Karena diagonal jajar genjang membagi jajar genjang menjadi dua segitiga siku-siku yang sama, maka keliling jajar genjang dapat dihitung dengan menjumlahkan panjang keempat sisi kedua segitiga tersebut. Hal ini menjadi dasar dari rumus keliling jajar genjang, yaitu K = 2(a + t), di mana a adalah panjang alas dan t adalah tinggi jajar genjang.
Memahami hubungan antara kongruen dan rumus jajar genjang sangat penting untuk dapat menghitung luas dan keliling jajar genjang dengan benar. Selain itu, pemahaman ini juga dapat membantu dalam menyelesaikan masalah-masalah yang berkaitan dengan jajar genjang, seperti menentukan luas tanah berbentuk jajar genjang atau menghitung panjang pagar yang mengelilingi taman berbentuk jajar genjang.
Pertanyaan Umum tentang Rumus Jajar Genjang
Rumus jajar genjang merupakan konsep penting dalam matematika yang digunakan untuk menghitung luas dan keliling bangun datar jajar genjang. Berikut adalah beberapa pertanyaan umum yang sering diajukan terkait dengan rumus jajar genjang:
Pertanyaan 1: Bagaimana cara menghitung luas jajar genjang?
Luas jajar genjang dapat dihitung menggunakan rumus L = a x t, dimana a adalah panjang alas dan t adalah tinggi jajar genjang.
Pertanyaan 2: Bagaimana cara menghitung keliling jajar genjang?
Keliling jajar genjang dapat dihitung menggunakan rumus K = 2(a + t), dimana a adalah panjang alas dan t adalah tinggi jajar genjang.
Pertanyaan 3: Apa saja sifat-sifat penting dari jajar genjang?
Jajar genjang memiliki beberapa sifat penting, antara lain:
- Sisi-sisi yang berhadapan sejajar dan sama panjang.
- Sudut-sudut yang berhadapan sama besar.
- Diagonal-diagonalnya saling membagi dua sama panjang.
Pertanyaan 4: Bagaimana cara menggunakan rumus jajar genjang dalam kehidupan sehari-hari?
Rumus jajar genjang dapat digunakan dalam berbagai aplikasi kehidupan sehari-hari, seperti:
- Menghitung luas tanah atau bangunan.
- Menghitung keliling pagar atau tembok.
- Menghitung luas kain atau kertas.
Demikian beberapa pertanyaan umum yang sering diajukan terkait dengan rumus jajar genjang. Memahami rumus dan konsep jajar genjang sangat penting untuk menyelesaikan berbagai masalah matematika dan juga untuk aplikasi praktis dalam kehidupan sehari-hari.
Selain memahami rumus jajar genjang, terdapat beberapa tips yang dapat membantu dalam menghitung luas dan keliling jajar genjang secara lebih efektif. Tips tersebut akan dibahas pada artikel selanjutnya.
Tips Menghitung Luas dan Keliling Jajar Genjang
Untuk menghitung luas dan keliling jajar genjang secara efektif, terdapat beberapa tips yang dapat diterapkan, yaitu:
Pastikan Mengidentifikasi Alas dan Tinggi Jajar Genjang dengan Benar
Alas dan tinggi jajar genjang merupakan besaran penting dalam rumus luas dan keliling jajar genjang. Pastikan untuk mengidentifikasi alas dan tinggi dengan benar agar hasil perhitungan tepat.
Gunakan Kalkulator atau Rumus yang Tepat
Gunakan kalkulator atau rumus yang tepat untuk menghitung luas dan keliling jajar genjang, yaitu L = a x t untuk luas dan K = 2(a + t) untuk keliling. pastikan untuk memasukkan nilai alas dan tinggi dengan benar.
Cek Kembali Hasil Perhitungan
Setelah menghitung luas dan keliling jajar genjang, luangkan waktu untuk memeriksa kembali hasil perhitungan. Hal ini penting untuk memastikan tidak ada kesalahan dalam proses perhitungan.
Pahami Konsep Jajar Genjang
Pemahaman yang baik tentang konsep jajar genjang, seperti sifat-sifat dan teorema yang terkait, akan sangat membantu dalam menyelesaikan masalah yang melibatkan jajar genjang.
Dengan menerapkan tips-tips ini, diharapkan proses menghitung luas dan keliling jajar genjang dapat dilakukan dengan lebih efektif dan akurat.
Kesimpulannya, rumus jajar genjang merupakan konsep penting dalam matematika yang banyak digunakan dalam berbagai aplikasi kehidupan sehari-hari. Dengan memahami rumus dan menerapkan tips-tips yang telah dibahas, kita dapat menghitung luas dan keliling jajar genjang secara efektif dan akurat.
Kesimpulan Rumus Jajar Genjang
Rumus jajar genjang merupakan konsep penting dalam matematika yang digunakan untuk menghitung luas dan keliling bangun datar jajar genjang. Rumus ini memiliki peran penting dalam berbagai aplikasi kehidupan sehari-hari, seperti menghitung luas tanah, keliling pagar, dan luas kain.
Dalam artikel ini, kita telah mengeksplorasi rumus jajar genjang, sifat-sifatnya, dan penggunaannya dalam menyelesaikan masalah. Kita juga membahas beberapa tips yang dapat membantu dalam menghitung luas dan keliling jajar genjang secara efektif.
Dengan memahami rumus jajar genjang dan menerapkan tips-tips yang telah dibahas, kita dapat menyelesaikan masalah yang berkaitan dengan jajar genjang dengan lebih mudah dan akurat. Pemahaman yang baik tentang konsep ini tidak hanya penting untuk menyelesaikan soal matematika, tetapi juga bermanfaat dalam berbagai aplikasi praktis dalam kehidupan sehari-hari.