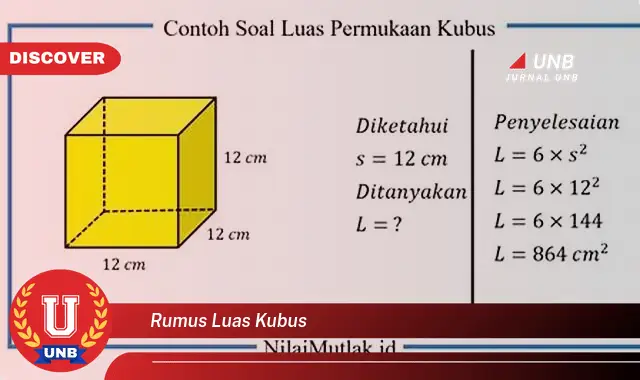
Rumus luas kubus adalah persamaan matematika yang digunakan untuk menghitung luas permukaan kubus. Rumus ini dinyatakan sebagai 6 x (sisi), dengan “sisi” mewakili panjang sisi kubus. Misalnya, jika panjang sisi kubus adalah 5 cm, maka luas permukaannya adalah 6 x (5 cm) = 150 cm.
Rumus luas kubus sangat penting karena memungkinkan kita untuk menghitung luas permukaan kubus dengan cepat dan mudah. Hal ini berguna dalam berbagai bidang, seperti arsitektur, teknik, dan desain. Selain itu, rumus ini memiliki sejarah yang panjang dan telah digunakan selama berabad-abad untuk menghitung luas permukaan kubus.
Dalam artikel ini, kita akan membahas secara mendalam tentang rumus luas kubus, termasuk cara menggunakannya, penerapannya, dan sejarahnya. Kita juga akan menjelajahi beberapa topik terkait, seperti volume kubus dan luas permukaan balok.
Rumus Luas Kubus
Rumus luas kubus sangat penting karena memiliki banyak kegunaan dalam kehidupan sehari-hari. Beberapa aspek pentingnya antara lain:
- Menghitung luas permukaan kubus
- Menghitung volume kubus
- Memecahkan masalah geometri
- Mendesain dan membangun struktur
- Mengemas dan mengangkut barang
- Menghitung luas permukaan balok
- Menganalisis data statistik
Dengan memahami rumus luas kubus, kita dapat memperoleh wawasan yang lebih dalam tentang berbagai aspek kehidupan dan lingkungan kita. Misalnya, kita dapat menggunakan rumus ini untuk menghitung luas permukaan sebuah ruangan atau volume sebuah kotak. Kita juga dapat menggunakannya untuk memecahkan masalah geometri, seperti mencari panjang diagonal sebuah kubus atau luas permukaan sebuah piramida. Selain itu, rumus luas kubus juga memiliki aplikasi dalam bidang arsitektur, teknik, dan desain.
Menghitung Luas Permukaan Kubus
Menghitung luas permukaan kubus merupakan salah satu aspek terpenting dalam memahami rumus luas kubus. Luas permukaan kubus adalah jumlah luas semua sisi kubus, dan rumus luas kubus memberikan cara yang sistematis untuk menghitung luas permukaan ini. Tanpa rumus ini, akan sangat sulit untuk menentukan luas permukaan kubus, terutama untuk kubus dengan ukuran besar atau kompleks.
Salah satu contoh penting di mana penghitungan luas permukaan kubus sangat penting adalah dalam bidang pengemasan dan pengangkutan. Perusahaan logistik perlu mengetahui luas permukaan kubus sebuah kotak untuk menentukan jumlah bahan kemasan yang dibutuhkan dan menghitung biaya pengiriman. Selain itu, dalam bidang arsitektur, penghitungan luas permukaan kubus sangat penting untuk menentukan jumlah bahan bangunan yang dibutuhkan dan memperkirakan biaya konstruksi sebuah bangunan.
Memahami hubungan antara menghitung luas permukaan kubus dan rumus luas kubus sangat penting untuk berbagai aplikasi praktis. Dengan memahami rumus ini, kita dapat menghitung luas permukaan kubus secara akurat dan efisien, yang pada akhirnya mengarah pada pengambilan keputusan yang lebih baik dan hasil yang lebih optimal dalam berbagai bidang.
Menghitung Volume Kubus
Menghitung volume kubus merupakan aspek penting lain yang terkait erat dengan rumus luas kubus. Volume kubus adalah ruang tiga dimensi yang ditempati oleh kubus, dan rumus luas kubus menyediakan dasar untuk menghitung volume ini. Memahami hubungan antara menghitung volume kubus dan rumus luas kubus sangat penting untuk berbagai aplikasi praktis.
-
Mendesain dan membangun struktur
Dalam bidang arsitektur dan teknik, menghitung volume kubus sangat penting untuk menentukan kapasitas ruang, merencanakan tata letak bangunan, dan memperkirakan jumlah bahan bangunan yang dibutuhkan.
-
Pengemasan dan pengangkutan
Dalam bidang logistik dan transportasi, menghitung volume kubus sangat penting untuk menentukan kapasitas kendaraan angkut, mengoptimalkan pemuatan barang, dan menghitung biaya pengiriman.
-
Analisis data statistik
Dalam bidang statistik, menghitung volume kubus sangat penting untuk menganalisis data tiga dimensi, seperti data populasi atau data ekonomi, dan memvisualisasikannya secara efektif.
-
Pemecahan masalah geometri
Dalam matematika dan geometri, menghitung volume kubus sangat penting untuk memecahkan masalah geometri yang kompleks, seperti mencari volume gabungan dari bangun ruang atau menghitung jarak antara dua titik dalam ruang tiga dimensi.
Dengan memahami hubungan antara menghitung volume kubus dan rumus luas kubus, kita dapat memperoleh wawasan yang lebih dalam tentang dunia di sekitar kita dan membuat keputusan yang lebih tepat dalam berbagai bidang. Rumus luas kubus tidak hanya berfungsi sebagai alat matematika tetapi juga sebagai dasar untuk memahami dan memanipulasi ruang tiga dimensi.
Memecahkan Masalah Geometri
Memecahkan masalah geometri merupakan salah satu aplikasi penting dari rumus luas kubus. Dalam geometri, kita sering dihadapkan pada masalah yang melibatkan menghitung luas permukaan atau volume kubus. Rumus luas kubus memberikan metode sistematis untuk menyelesaikan masalah ini secara akurat dan efisien.
Salah satu contoh nyata di mana rumus luas kubus digunakan untuk memecahkan masalah geometri adalah dalam desain dan konstruksi. Arsitek dan insinyur menggunakan rumus ini untuk menghitung luas permukaan dan volume bangunan, sehingga mereka dapat merencanakan tata letak, memperkirakan biaya bahan, dan memastikan stabilitas struktural. Contoh lainnya adalah dalam pengemasan dan transportasi, di mana rumus luas kubus digunakan untuk menentukan ukuran kemasan yang optimal dan menghitung biaya pengiriman.
Memahami hubungan antara rumus luas kubus dan pemecahan masalah geometri sangat penting untuk berbagai bidang. Dengan memahami rumus ini, kita dapat memecahkan masalah geometri secara efektif, mengoptimalkan desain dan konstruksi, serta membuat keputusan yang tepat dalam industri pengemasan dan transportasi.
Mendesain dan membangun struktur
Rumus luas kubus berperan penting dalam mendesain dan membangun struktur. Ini digunakan untuk menghitung luas permukaan dan volume bangunan, yang sangat penting untuk perencanaan tata letak, estimasi biaya bahan, dan memastikan stabilitas struktural.
-
Perencanaan Tata Letak
Rumus luas kubus digunakan untuk menentukan luas permukaan keseluruhan bangunan, yang sangat penting untuk merencanakan tata letak interior dan eksterior. Hal ini memungkinkan arsitek dan insinyur untuk mengoptimalkan penggunaan ruang, menempatkan ruangan dan fitur secara efisien, dan memastikan aliran yang lancar di seluruh bangunan.
-
Estimasi Biaya Bahan
Menghitung volume bangunan menggunakan rumus luas kubus sangat penting untuk memperkirakan biaya bahan yang dibutuhkan untuk konstruksi. Dengan mengetahui volume bangunan, arsitek dan insinyur dapat menghitung jumlah bahan yang tepat, seperti beton, baja, dan kayu, yang diperlukan untuk menyelesaikan proyek. Hal ini membantu mengendalikan biaya dan memastikan alokasi anggaran yang tepat.
-
Memastikan Stabilitas Struktural
Rumus luas kubus juga digunakan untuk menganalisis stabilitas struktural bangunan. Dengan menghitung luas permukaan dan volume bagian yang berbeda dari bangunan, insinyur dapat menilai kekuatan dan integritas strukturalnya. Hal ini sangat penting untuk memastikan keamanan dan ketahanan bangunan terhadap beban dan gaya eksternal, seperti gempa bumi dan angin.
Memahami hubungan antara rumus luas kubus dan desain serta konstruksi struktur sangatlah penting. Rumus ini menyediakan dasar untuk perencanaan tata letak yang optimal, estimasi biaya bahan yang akurat, dan analisis stabilitas struktural yang komprehensif. Dengan demikian, rumus luas kubus sangat penting untuk memastikan keberhasilan dan keamanan proyek desain dan konstruksi.
Mengemas dan Mengangkut Barang
Dalam bidang logistik dan transportasi, rumus luas kubus berperan penting dalam mengemas dan mengangkut barang. Ini digunakan untuk menghitung volume dan luas permukaan kemasan, yang sangat penting untuk mengoptimalkan penggunaan ruang, meminimalkan biaya pengiriman, dan memastikan keamanan barang selama pengangkutan.
-
Mengoptimalkan Penggunaan Ruang
Rumus luas kubus digunakan untuk menentukan ukuran kemasan yang optimal, sehingga barang dapat dikemas secara efisien dan aman. Dengan menghitung volume barang, perusahaan logistik dapat memilih kemasan dengan ukuran yang tepat, meminimalkan ruang kosong dan mengoptimalkan kapasitas kendaraan angkut.
-
Meminimalkan Biaya Pengiriman
Biaya pengiriman sering kali dihitung berdasarkan volume dan berat barang. Dengan menggunakan rumus luas kubus untuk menghitung volume kemasan, perusahaan logistik dapat menentukan berat volumetrik barang dan mengoptimalkan metode pengiriman untuk meminimalkan biaya.
-
Memastikan Keamanan Barang
Kemasan yang dirancang dengan baik sangat penting untuk memastikan keamanan barang selama pengangkutan. Rumus luas kubus digunakan untuk menghitung luas permukaan kemasan, sehingga perusahaan logistik dapat memilih bahan kemasan yang tepat untuk melindungi barang dari kerusakan, kelembaban, dan guncangan.
Memahami hubungan antara rumus luas kubus dan pengemasan serta pengangkutan barang sangatlah penting. Rumus ini menyediakan dasar untuk mengoptimalkan penggunaan ruang, meminimalkan biaya pengiriman, dan memastikan keamanan barang selama pengangkutan. Dengan demikian, rumus luas kubus sangat penting untuk kelancaran dan efisiensi rantai pasokan global.
Menghitung Luas Permukaan Balok
Menghitung luas permukaan balok merupakan aspek penting yang terkait dengan rumus luas kubus. Balok adalah prisma segi enam yang memiliki dua sisi alas yang berbentuk persegi atau persegi panjang. Luas permukaan balok terdiri dari luas kedua alas dan luas selimutnya, yang merupakan jumlah luas semua sisi tegak balok.
Rumus luas kubus dapat digunakan untuk menghitung luas permukaan balok dengan cara membagi balok menjadi kubus-kubus kecil. Luas permukaan setiap kubus kecil dapat dihitung menggunakan rumus luas kubus, dan kemudian luas permukaan keseluruhan balok dapat diperoleh dengan menjumlahkan luas permukaan semua kubus kecil tersebut.
Memahami hubungan antara menghitung luas permukaan balok dan rumus luas kubus sangat penting dalam berbagai aplikasi praktis. Misalnya, dalam bidang konstruksi, rumus luas kubus digunakan untuk menghitung luas permukaan dinding dan lantai bangunan. Dalam bidang pengemasan, rumus luas kubus digunakan untuk menghitung luas permukaan kotak dan kardus untuk menentukan biaya bahan kemasan dan pengiriman.
Menganalisis Data Statistik
Rumus luas kubus memiliki keterkaitan yang erat dengan analisis data statistik, khususnya dalam konteks analisis data tiga dimensi dan visualisasi data. Berikut adalah beberapa aspek penting mengenai keterkaitan tersebut:
-
Memvisualisasikan Data Tiga Dimensi
Rumus luas kubus dapat digunakan untuk membuat representasi visual dari data tiga dimensi. Misalnya, dalam bidang kesehatan, rumus luas kubus dapat digunakan untuk memvisualisasikan distribusi spasial penyakit dalam suatu populasi atau untuk memodelkan pertumbuhan tumor. Visualisasi ini sangat penting untuk mengidentifikasi pola dan tren dalam data, serta untuk mengomunikasikan temuan dengan jelas.
-
Menganalisis Data Spasial
Rumus luas kubus juga berguna untuk menganalisis data spasial, seperti data populasi atau data ekonomi. Dengan menggunakan rumus luas kubus, peneliti dapat menghitung volume ruang yang ditempati oleh data dan mengidentifikasi area dengan kepadatan tinggi atau rendah. Analisis ini sangat penting untuk perencanaan kota, manajemen sumber daya, dan pengambilan keputusan berdasarkan bukti.
-
Membangun Model Statistik
Rumus luas kubus dapat digunakan untuk membangun model statistik yang kompleks, seperti model prediksi atau model simulasi. Model-model ini dapat digunakan untuk memprediksi tren masa depan, mengoptimalkan proses, atau mensimulasikan skenario hipotetis. Memahami hubungan antara rumus luas kubus dan pembangunan model statistik sangat penting untuk pengembangan solusi berbasis data yang efektif.
-
Mengevaluasi Model Statistik
Rumus luas kubus juga dapat digunakan untuk mengevaluasi kinerja model statistik. Dengan menghitung luas permukaan atau volume model, peneliti dapat menilai akurasi dan kecocokannya dengan data yang diamati. Evaluasi ini sangat penting untuk memastikan bahwa model yang dibangun valid dan dapat diandalkan untuk pengambilan keputusan.
Secara keseluruhan, rumus luas kubus memainkan peran penting dalam analisis data statistik, khususnya dalam konteks data tiga dimensi dan visualisasi data. Dengan memahami hubungan ini, peneliti dapat menggunakan rumus luas kubus untuk memperoleh wawasan yang lebih dalam dari data, membuat keputusan yang lebih tepat, dan mengomunikasikan temuan mereka secara efektif.
Pertanyaan Umum tentang Rumus Luas Kubus
Berikut beberapa pertanyaan umum beserta jawabannya mengenai rumus luas kubus:
Pertanyaan 1: Apa itu rumus luas kubus dan bagaimana cara menggunakannya?
Rumus luas kubus adalah persamaan matematika yang digunakan untuk menghitung luas permukaan kubus. Rumus ini dinyatakan sebagai Luas permukaan = 6 x (sisi2), di mana “sisi” adalah panjang sisi kubus. Untuk menggunakan rumus ini, cukup substitusikan panjang sisi kubus ke dalam rumus dan hitung hasilnya.
Pertanyaan 2: Mengapa penting untuk memahami rumus luas kubus?
Memahami rumus luas kubus sangat penting karena memungkinkan kita menghitung luas permukaan kubus dengan cepat dan mudah. Hal ini berguna dalam berbagai bidang, seperti arsitektur, teknik, dan desain. Selain itu, rumus ini memiliki sejarah yang panjang dan telah digunakan selama berabad-abad untuk menghitung luas permukaan kubus.
Pertanyaan 3: Apa saja aplikasi praktis dari rumus luas kubus?
Rumus luas kubus memiliki banyak aplikasi praktis, di antaranya menghitung luas permukaan kubus, menghitung volume kubus, memecahkan masalah geometri, mendesain dan membangun struktur, mengemas dan mengangkut barang, serta menganalisis data statistik.
Pertanyaan 4: Bagaimana rumus luas kubus terkait dengan konsep matematika lainnya?
Rumus luas kubus terkait dengan konsep matematika lainnya, seperti luas permukaan balok dan volume kubus. Rumus ini juga dapat digunakan untuk membangun model statistik dan mengevaluasi kinerja model tersebut.
Kesimpulannya, rumus luas kubus adalah alat matematika yang penting dan berguna dengan berbagai aplikasi dalam kehidupan sehari-hari. Memahami rumus ini sangat penting untuk memecahkan masalah geometri, merancang dan membangun struktur, serta menganalisis data statistik.
Untuk mempelajari lebih lanjut tentang rumus luas kubus, silakan baca artikel Tips Menggunakan Rumus Luas Kubus yang disediakan di bawah ini.
Tips Menggunakan Rumus Luas Kubus
Untuk menggunakan rumus luas kubus secara efektif dan akurat, perhatikan beberapa tips berikut:
Tip 1: Pahami Konsep Sisi Kubus
Dalam rumus luas kubus, “sisi” mengacu pada panjang rusuk atau tepi kubus. Pastikan untuk mengukur dan menggunakan panjang sisi yang benar saat menghitung luas permukaan.
Tip 2: Gunakan Unit yang Konsisten
Saat menghitung luas permukaan kubus, penting untuk menggunakan unit yang konsisten untuk panjang sisi. Misalnya, jika Anda mengukur sisi dalam sentimeter, maka hasil luas permukaan juga akan dalam sentimeter persegi.
Tip 3: Perhatikan Tanda Kurung
Dalam rumus luas kubus, terdapat tanda kurung yang menunjukkan bahwa panjang sisi harus dikuadratkan terlebih dahulu sebelum dikalikan dengan 6. Pastikan untuk mengikuti urutan operasi yang benar.
Tip 4: Gunakan Kalkulator untuk Akurasi
Untuk memastikan akurasi perhitungan, terutama untuk kubus dengan sisi yang panjang, disarankan untuk menggunakan kalkulator untuk menghitung pangkat dua dan perkalian.
Dengan mengikuti tips ini, Anda dapat menggunakan rumus luas kubus dengan percaya diri untuk menghitung luas permukaan kubus secara akurat dan efisien.
Dengan memahami rumus luas kubus dan menggunakan tips ini, Anda akan dapat memecahkan masalah geometri, merancang dan membangun struktur, serta menganalisis data statistik dengan lebih efektif.
Kesimpulan tentang Rumus Luas Kubus
Dalam artikel ini, kita telah mengeksplorasi secara mendalam tentang rumus luas kubus, termasuk cara menggunakannya, penerapannya, dan sejarahnya. Kita telah belajar bahwa rumus luas kubus adalah alat matematika yang penting dan berguna dengan berbagai aplikasi dalam kehidupan sehari-hari.
Dengan memahami rumus luas kubus dan menggunakannya secara efektif, kita dapat memecahkan masalah geometri, merancang dan membangun struktur, serta menganalisis data statistik dengan lebih akurat dan efisien. Penguasaan rumus ini sangat penting bagi para siswa, praktisi di bidang arsitektur, teknik, dan logistik, serta siapa pun yang ingin memiliki pemahaman yang lebih dalam tentang konsep matematika dan penerapannya dalam kehidupan nyata.



















