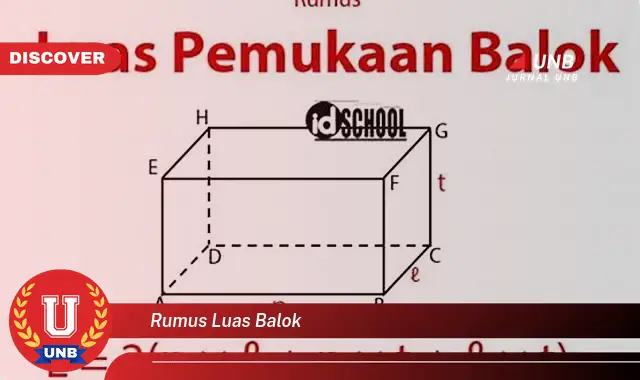
Rumus luas balok adalah rumus yang digunakan untuk menghitung luas permukaan balok. Rumus ini menyatakan bahwa luas permukaan balok sama dengan dua kali jumlah hasil kali panjang, lebar, dan tinggi balok. Secara matematis, rumus luas balok dapat ditulis sebagai berikut:
L = 2 x (p x l + p x t + l x t)
dengan L adalah luas permukaan balok, p adalah panjang balok, l adalah lebar balok, dan t adalah tinggi balok. Rumus luas balok ini sangat penting dalam berbagai bidang, seperti arsitektur, teknik sipil, dan desain interior. Dengan menggunakan rumus ini, kita dapat menghitung luas permukaan balok dengan mudah dan akurat.
Selain itu, rumus luas balok juga memiliki beberapa manfaat. Pertama, rumus ini dapat digunakan untuk menghitung luas permukaan balok dengan berbagai ukuran dan bentuk. Kedua, rumus ini mudah diingat dan diterapkan. Ketiga, rumus ini dapat digunakan untuk menyelesaikan berbagai masalah yang berkaitan dengan balok.
Dalam sejarahnya, rumus luas balok telah mengalami perkembangan yang panjang. Pada awalnya, rumus ini hanya digunakan untuk menghitung luas permukaan balok yang berbentuk kubus. Namun, seiring dengan berkembangnya ilmu pengetahuan dan teknologi, rumus ini kemudian diperluas untuk dapat digunakan menghitung luas permukaan balok dengan berbagai bentuk.
Saat ini, rumus luas balok telah menjadi salah satu rumus dasar yang diajarkan dalam matematika. Rumus ini sangat penting untuk dipahami dan dikuasai, karena memiliki banyak aplikasi dalam kehidupan sehari-hari.
rumus luas balok
Rumus luas balok adalah rumus yang sangat penting dalam berbagai bidang, seperti arsitektur, teknik sipil, dan desain interior. Rumus ini digunakan untuk menghitung luas permukaan balok, yaitu jumlah seluruh permukaan balok. Berikut adalah 7 aspek penting yang terkait dengan rumus luas balok:
- Panjang
- Lebar
- Tinggi
- Luas
- Permukaan
- Bangunan
- Konstruksi
Panjang, lebar, dan tinggi merupakan tiga dimensi dasar yang digunakan untuk menghitung luas permukaan balok. Luas adalah hasil perkalian dari panjang, lebar, dan tinggi. Permukaan balok terdiri dari enam sisi, yaitu dua sisi alas, dua sisi samping, dan dua sisi atas. Bangunan dan konstruksi merupakan bidang di mana rumus luas balok banyak digunakan, misalnya untuk menghitung luas permukaan dinding, lantai, dan atap.
Panjang
Panjang merupakan salah satu dimensi penting dalam rumus luas balok. Panjang mewakili jarak dari ujung ke ujung balok pada sisi terpanjang. Dalam rumus luas balok, panjang dikalikan dengan lebar dan tinggi untuk menghitung luas permukaan balok.
Panjang sangat penting karena mempengaruhi luas permukaan balok. Semakin panjang balok, semakin besar luas permukaannya. Hal ini karena panjang merupakan faktor pengali dalam rumus luas balok. Misalnya, sebuah balok dengan panjang 10 cm, lebar 5 cm, dan tinggi 3 cm memiliki luas permukaan 90 cm2. Jika panjang balok tersebut ditambah menjadi 15 cm, maka luas permukaannya menjadi 120 cm2.
Memahami hubungan antara panjang dan rumus luas balok sangat penting dalam berbagai aplikasi praktis. Misalnya, dalam arsitektur, panjang digunakan untuk menghitung luas permukaan dinding, lantai, dan atap. Dalam teknik sipil, panjang digunakan untuk menghitung luas permukaan jembatan, jalan, dan terowongan.
Dengan memahami hubungan antara panjang dan rumus luas balok, kita dapat menghitung luas permukaan balok dengan akurat dan cepat. Hal ini penting untuk memastikan bahwa struktur yang kita bangun memiliki luas permukaan yang sesuai dengan kebutuhan.
Lebar
Lebar merupakan salah satu dimensi penting dalam rumus luas balok. Lebar mewakili jarak dari sisi ke sisi balok pada sisi terlebar. Dalam rumus luas balok, lebar dikalikan dengan panjang dan tinggi untuk menghitung luas permukaan balok.
-
Pengaruh Lebar pada Luas Permukaan
Lebar sangat penting karena mempengaruhi luas permukaan balok. Semakin lebar balok, semakin besar luas permukaannya. Hal ini karena lebar merupakan faktor pengali dalam rumus luas balok. Misalnya, sebuah balok dengan panjang 10 cm, lebar 5 cm, dan tinggi 3 cm memiliki luas permukaan 90 cm2. Jika lebar balok tersebut ditambah menjadi 10 cm, maka luas permukaannya menjadi 150 cm2.
-
Aplikasi Praktis Lebar
Memahami hubungan antara lebar dan rumus luas balok sangat penting dalam berbagai aplikasi praktis. Misalnya, dalam arsitektur, lebar digunakan untuk menghitung luas permukaan dinding, lantai, dan atap. Dalam teknik sipil, lebar digunakan untuk menghitung luas permukaan jembatan, jalan, dan terowongan.
-
Contoh Dampak Lebar
Lebar juga dapat mempengaruhi biaya dan waktu konstruksi. Misalnya, sebuah bangunan dengan lebar yang lebih besar akan membutuhkan lebih banyak bahan dan tenaga kerja untuk dibangun, sehingga biaya dan waktu konstruksinya akan lebih besar.
-
Kesimpulan
Dengan memahami hubungan antara lebar dan rumus luas balok, kita dapat menghitung luas permukaan balok dengan akurat dan cepat. Hal ini penting untuk memastikan bahwa struktur yang kita bangun memiliki luas permukaan yang sesuai dengan kebutuhan dan meminimalkan biaya serta waktu konstruksi.
Tinggi
Tinggi merupakan dimensi penting lainnya dalam rumus luas balok. Tinggi mewakili jarak dari alas ke atas balok. Dalam rumus luas balok, tinggi dikalikan dengan panjang dan lebar untuk menghitung luas permukaan balok.
-
Pengaruh Tinggi pada Luas Permukaan
Tinggi sangat penting karena mempengaruhi luas permukaan balok. Semakin tinggi balok, semakin besar luas permukaannya. Hal ini karena tinggi merupakan faktor pengali dalam rumus luas balok. Misalnya, sebuah balok dengan panjang 10 cm, lebar 5 cm, dan tinggi 3 cm memiliki luas permukaan 90 cm2. Jika tinggi balok tersebut ditambah menjadi 6 cm, maka luas permukaannya menjadi 120 cm2.
-
Aplikasi Praktis Tinggi
Memahami hubungan antara tinggi dan rumus luas balok sangat penting dalam berbagai aplikasi praktis. Misalnya, dalam arsitektur, tinggi digunakan untuk menghitung luas permukaan dinding, lantai, dan atap. Dalam teknik sipil, tinggi digunakan untuk menghitung luas permukaan jembatan, jalan, dan terowongan.
-
Contoh Dampak Tinggi
Tinggi juga dapat mempengaruhi biaya dan waktu konstruksi. Misalnya, sebuah bangunan dengan tinggi yang lebih besar akan membutuhkan lebih banyak bahan dan tenaga kerja untuk dibangun, sehingga biaya dan waktu konstruksinya akan lebih besar.
-
Kesimpulan
Dengan memahami hubungan antara tinggi dan rumus luas balok, kita dapat menghitung luas permukaan balok dengan akurat dan cepat. Hal ini penting untuk memastikan bahwa struktur yang kita bangun memiliki luas permukaan yang sesuai dengan kebutuhan dan meminimalkan biaya serta waktu konstruksi.
Luas
Luas merupakan besaran yang menyatakan ukuran permukaan suatu benda. Dalam konteks rumus luas balok, luas mengacu pada luas permukaan balok, yaitu jumlah seluruh permukaan balok. Luas permukaan balok sangat penting karena digunakan untuk menghitung berbagai hal, seperti kebutuhan cat, wallpaper, atau bahan pelapis lainnya.
Rumus luas balok menghubungkan luas dengan dimensi balok, yaitu panjang, lebar, dan tinggi. Rumus ini menyatakan bahwa luas permukaan balok sama dengan dua kali jumlah hasil kali panjang, lebar, dan tinggi balok. Memahami hubungan ini sangat penting untuk menghitung luas permukaan balok dengan benar.
Sebagai contoh, sebuah balok dengan panjang 10 cm, lebar 5 cm, dan tinggi 3 cm memiliki luas permukaan 90 cm2. Luas permukaan ini dapat dihitung menggunakan rumus luas balok, yaitu L = 2 x (p x l + p x t + l x t) = 2 x (10 cm x 5 cm + 10 cm x 3 cm + 5 cm x 3 cm) = 90 cm2.
Dengan memahami hubungan antara luas dan rumus luas balok, kita dapat menghitung luas permukaan balok dengan akurat dan cepat. Hal ini penting untuk berbagai aplikasi praktis, seperti arsitektur, teknik sipil, dan desain interior.
Permukaan
Permukaan merupakan salah satu aspek penting yang terkait dengan rumus luas balok. Permukaan balok mengacu pada seluruh sisi luar balok, termasuk alas, sisi samping, dan sisi atas. Memahami permukaan balok sangat penting karena mempengaruhi luas permukaan balok.
-
Jenis-jenis Permukaan Balok
Balok memiliki enam permukaan, yaitu dua permukaan alas, dua permukaan samping, dan dua permukaan atas. Setiap permukaan memiliki bentuk dan ukuran yang berbeda, tergantung pada dimensi balok.
-
Pengaruh Permukaan pada Luas Permukaan
Luas permukaan balok dipengaruhi oleh luas masing-masing permukaan. Semakin besar luas permukaan balok, semakin besar pula luas permukaan balok secara keseluruhan. Hal ini karena luas permukaan balok merupakan penjumlahan luas seluruh permukaan balok.
-
Aplikasi Praktis Permukaan Balok
Memahami jenis-jenis permukaan balok dan pengaruhnya terhadap luas permukaan balok sangat penting dalam berbagai aplikasi praktis, seperti arsitektur, teknik sipil, dan desain interior. Misalnya, dalam arsitektur, luas permukaan balok digunakan untuk menghitung kebutuhan cat, wallpaper, atau bahan pelapis lainnya.
-
Kesimpulan
Dengan memahami permukaan balok dan pengaruhnya terhadap luas permukaan balok, kita dapat menghitung luas permukaan balok dengan akurat dan cepat. Hal ini penting untuk berbagai aplikasi praktis, seperti arsitektur, teknik sipil, dan desain interior.
Bangunan
Bangunan merupakan struktur fisik yang dibuat untuk berbagai keperluan, seperti tempat tinggal, perkantoran, atau tempat ibadah. Dalam konteks rumus luas balok, bangunan memiliki hubungan yang erat karena rumus tersebut digunakan untuk menghitung luas permukaan bangunan.
Luas permukaan bangunan sangat penting karena mempengaruhi berbagai aspek, seperti kebutuhan bahan bangunan, biaya konstruksi, dan efisiensi energi. Dengan menghitung luas permukaan bangunan secara akurat menggunakan rumus luas balok, kita dapat merencanakan dan membangun bangunan yang sesuai dengan kebutuhan dan anggaran.
Sebagai contoh, dalam pembangunan sebuah rumah, rumus luas balok digunakan untuk menghitung luas permukaan dinding, lantai, dan atap. Luas permukaan ini kemudian digunakan untuk menentukan jumlah bahan bangunan yang dibutuhkan, seperti batu bata, semen, dan cat. Selain itu, luas permukaan bangunan juga digunakan untuk menghitung biaya konstruksi dan memperkirakan biaya energi yang dibutuhkan untuk mengoperasikan bangunan tersebut.
Memahami hubungan antara bangunan dan rumus luas balok sangat penting bagi arsitek, insinyur sipil, dan kontraktor. Dengan pemahaman ini, mereka dapat merancang dan membangun bangunan yang efisien, estetis, dan sesuai dengan kebutuhan.
Konstruksi
Konstruksi merupakan proses membangun atau membuat suatu struktur fisik, seperti gedung, jembatan, atau jalan. Dalam konteks rumus luas balok, konstruksi memiliki keterkaitan yang erat karena rumus tersebut digunakan untuk menghitung luas permukaan struktur yang akan dibangun.
Luas permukaan struktur sangat penting dalam konstruksi karena mempengaruhi berbagai aspek, seperti kebutuhan material, biaya pembangunan, dan efisiensi energi. Dengan menghitung luas permukaan struktur secara akurat menggunakan rumus luas balok, maka dapat direncanakan dan dibangun struktur yang sesuai dengan kebutuhan dan anggaran.
Sebagai contoh, dalam pembangunan gedung, rumus luas balok digunakan untuk menghitung luas permukaan dinding, lantai, dan atap. Luas permukaan ini kemudian digunakan untuk menentukan jumlah material bangunan yang dibutuhkan, seperti batu bata, semen, dan cat. Selain itu, luas permukaan gedung juga digunakan untuk menghitung biaya pembangunan dan memperkirakan biaya energi yang dibutuhkan untuk mengoperasikan gedung tersebut.
Memahami hubungan antara konstruksi dan rumus luas balok sangat penting bagi arsitek, insinyur sipil, dan kontraktor. Dengan pemahaman ini, mereka dapat merancang dan membangun struktur yang efisien, estetis, dan sesuai dengan kebutuhan.
Pertanyaan Umum tentang Rumus Luas Balok
Bagian ini berisi beberapa pertanyaan umum dan jawabannya terkait dengan rumus luas balok. Rumus luas balok digunakan untuk menghitung luas permukaan balok, yang penting untuk berbagai keperluan, seperti arsitektur, teknik sipil, dan desain interior.
Pertanyaan 1: Apa saja dimensi yang diperlukan untuk menghitung luas permukaan balok menggunakan rumus luas balok?
Jawaban: Untuk menghitung luas permukaan balok menggunakan rumus luas balok, diperlukan tiga dimensi, yaitu panjang, lebar, dan tinggi balok.
Pertanyaan 2: Bagaimana rumus luas balok dapat diaplikasikan dalam kehidupan sehari-hari?
Jawaban: Rumus luas balok dapat diaplikasikan dalam berbagai aspek kehidupan sehari-hari, seperti menghitung kebutuhan cat untuk mengecat dinding rumah, menghitung biaya ubin untuk lantai, atau menghitung volume air yang dapat ditampung dalam sebuah bak mandi.
Pertanyaan 3: Apa pentingnya memahami rumus luas balok dalam bidang arsitektur dan teknik sipil?
Jawaban: Dalam bidang arsitektur dan teknik sipil, memahami rumus luas balok sangat penting untuk menghitung luas permukaan bangunan, jembatan, atau struktur lainnya. Luas permukaan ini digunakan untuk menentukan kebutuhan material, biaya konstruksi, dan efisiensi energi.
Pertanyaan 4: Apakah ada cara mudah untuk menghafal rumus luas balok?
Jawaban: Salah satu cara mudah untuk menghafal rumus luas balok adalah dengan menggunakan singkatan “2PLT”, yang merupakan singkatan dari “dua kali panjang, lebar, dan tinggi”.
Kesimpulan
Rumus luas balok merupakan rumus yang penting untuk dipahami dan dikuasai karena memiliki banyak aplikasi dalam kehidupan sehari-hari, terutama dalam bidang arsitektur, teknik sipil, dan desain interior.
Dengan memahami rumus luas balok, kita dapat menghitung luas permukaan balok dengan akurat dan cepat, sehingga dapat menghemat waktu dan biaya dalam berbagai proyek.
Selain itu, memahami rumus luas balok juga dapat membantu kita dalam memahami konsep matematika dasar, seperti luas permukaan dan volume. Oleh karena itu, sangat disarankan untuk mempelajari dan memahami rumus luas balok dengan baik.
Untuk informasi lebih lanjut dan tips tentang cara menggunakan rumus luas balok, silakan baca artikel selanjutnya.
Tips Menggunakan Rumus Luas Balok
Rumus luas balok adalah rumus yang digunakan untuk menghitung luas permukaan balok. Rumus ini memiliki banyak aplikasi dalam kehidupan sehari-hari, terutama dalam bidang arsitektur, teknik sipil, dan desain interior.
Tip 1: Pahami Konsep Dimensi Balok
Untuk menggunakan rumus luas balok dengan benar, penting untuk memahami konsep dimensi balok. Balok memiliki tiga dimensi, yaitu panjang, lebar, dan tinggi. Pastikan untuk mengukur ketiga dimensi ini dengan akurat sebelum menghitung luas permukaan balok.
Tip 2: Gunakan Rumus yang Tepat
Rumus luas balok adalah L = 2 x (p x l + p x t + l x t), dengan L adalah luas permukaan balok, p adalah panjang balok, l adalah lebar balok, dan t adalah tinggi balok. Pastikan untuk menggunakan rumus yang tepat ini untuk menghitung luas permukaan balok.
Tip 3: Periksa Hasil Perhitungan
Setelah menghitung luas permukaan balok, periksa kembali hasil perhitungan Anda untuk memastikan akurasinya. Anda dapat melakukan pengecekan dengan menggunakan rumus luas balok sekali lagi dengan nilai dimensi yang berbeda.
Tip 4: Terapkan dalam Praktik
Rumus luas balok dapat diterapkan dalam berbagai situasi praktis. Misalnya, Anda dapat menggunakan rumus ini untuk menghitung kebutuhan cat untuk mengecat dinding rumah, menghitung biaya ubin untuk lantai, atau menghitung volume air yang dapat ditampung dalam sebuah bak mandi.
Dengan mengikuti tips ini, Anda dapat menggunakan rumus luas balok dengan efektif dan akurat.
Kesimpulan
Rumus luas balok adalah rumus yang penting untuk dipahami dan dikuasai karena memiliki banyak aplikasi dalam kehidupan sehari-hari. Dengan memahami dan menerapkan tips yang telah dijelaskan, Anda dapat menggunakan rumus luas balok dengan percaya diri dan efisien.
Kesimpulan Rumus Luas Balok
Rumus luas balok merupakan rumus penting yang banyak digunakan dalam berbagai bidang, seperti arsitektur, teknik sipil, dan desain interior. Rumus ini digunakan untuk menghitung luas permukaan balok, yang merupakan jumlah seluruh permukaan balok.
Pemahaman tentang rumus luas balok sangat penting karena dapat membantu kita dalam berbagai hal, seperti menentukan kebutuhan material, menghitung biaya konstruksi, dan mengestimasi volume air yang dapat ditampung dalam suatu wadah berbentuk balok. Selain itu, rumus ini juga dapat digunakan untuk menyelesaikan berbagai masalah matematika yang berkaitan dengan balok.
Dengan memahami dan menguasai rumus luas balok, kita dapat mengerjakan berbagai tugas dan proyek dengan lebih efektif dan efisien. Oleh karena itu, sangat disarankan untuk mempelajari dan memahami rumus ini dengan baik.



















