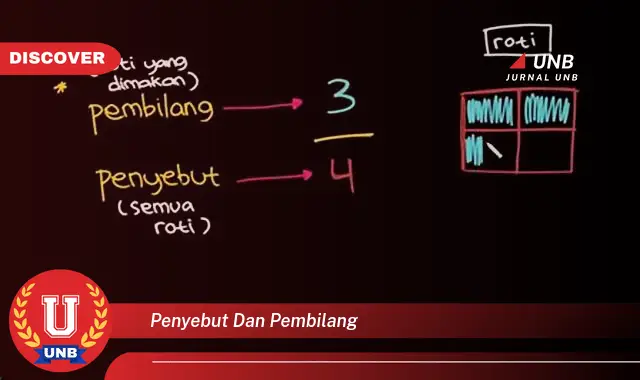
Penyebut dan pembilang adalah dua komponen penting dalam matematika, khususnya pada operasi pecahan. Penyebut terletak di bagian bawah pecahan, sedangkan pembilang terletak di bagian atas. Penyebut menunjukkan jumlah bagian yang sama dalam keseluruhan, sementara pembilang menunjukkan banyaknya bagian yang diambil.
Misalnya, pada pecahan 1/2, penyebutnya adalah 2 dan pembilangnya adalah 1. Ini berarti bahwa keseluruhan dibagi menjadi 2 bagian yang sama, dan 1 dari bagian tersebut diambil.
Penyebut dan pembilang sangat penting dalam memahami operasi pecahan, seperti penjumlahan, pengurangan, perkalian, dan pembagian. Memahami konsep penyebut dan pembilang menjadi dasar bagi pemahaman matematika yang lebih kompleks.
Penyebut dan Pembilang
Penyebut dan pembilang merupakan komponen penting dalam matematika, khususnya pada operasi pecahan. Memahami konsep penyebut dan pembilang menjadi dasar bagi pemahaman matematika yang lebih kompleks.
- Bagian bawah pecahan
- Bagian atas pecahan
- Menunjukkan jumlah bagian
- Menunjukkan banyaknya bagian
- Penting untuk operasi pecahan
- Dasar matematika yang kompleks
- Contoh: 1/2 (penyebut: 2, pembilang: 1)
Penyebut dan pembilang sangat penting dalam memahami operasi pecahan, seperti penjumlahan, pengurangan, perkalian, dan pembagian. Memahami konsep penyebut dan pembilang menjadi dasar bagi pemahaman matematika yang lebih kompleks. Misalnya, dalam penjumlahan pecahan, penyebut harus disamakan terlebih dahulu agar pecahan dapat dijumlahkan. Konsep penyebut dan pembilang juga terkait erat dengan konsep kesetaraan pecahan, yaitu pecahan yang memiliki nilai yang sama meskipun penyebut dan pembilangnya berbeda.
Bagian bawah pecahan
Bagian bawah pecahan disebut penyebut. Penyebut menunjukkan jumlah bagian yang sama dalam keseluruhan. Misalnya, pada pecahan 1/2, penyebutnya adalah 2, yang berarti bahwa keseluruhan dibagi menjadi 2 bagian yang sama.
Penyebut sangat penting dalam operasi pecahan. Misalnya, dalam penjumlahan pecahan, penyebut harus disamakan terlebih dahulu agar pecahan dapat dijumlahkan. Jika penyebutnya berbeda, maka perlu dicari kelipatan persekutuan terkecil (KPK) dari penyebut-penyebut tersebut.
Memahami konsep penyebut sangat penting untuk memahami matematika yang lebih kompleks, seperti aljabar dan kalkulus. Penyebut juga memiliki aplikasi dalam kehidupan nyata, seperti dalam mengukur panjang, berat, dan waktu.
Bagian atas pecahan
Bagian atas pecahan disebut pembilang. Pembilang menunjukkan banyaknya bagian yang diambil dari keseluruhan. Misalnya, pada pecahan 1/2, pembilangnya adalah 1, yang berarti bahwa 1 dari 2 bagian yang sama diambil.
-
Peran pembilang
Pembilang menunjukkan banyaknya bagian dari keseluruhan yang diwakili oleh pecahan. Misalnya, dalam pecahan 3/4, pembilangnya adalah 3, yang berarti bahwa pecahan tersebut mewakili 3 dari 4 bagian yang sama.
-
Contoh dalam kehidupan nyata
Pembilang digunakan dalam berbagai situasi kehidupan nyata. Misalnya, dalam resep memasak, pembilang menunjukkan jumlah bahan yang dibutuhkan. Dalam pengukuran, pembilang menunjukkan bagian dari satuan yang diukur.
-
Implikasi dalam konteks penyebut dan pembilang
Pembilang dan penyebut bersama-sama menentukan nilai pecahan. Pecahan dengan penyebut yang sama dapat dibandingkan nilainya berdasarkan pembilangnya. Pembilang juga digunakan dalam operasi pecahan, seperti penjumlahan, pengurangan, perkalian, dan pembagian.
Dengan memahami konsep pembilang dan penyebut, kita dapat memahami dan menggunakan pecahan dengan lebih efektif. Pecahan merupakan dasar dari banyak konsep matematika yang lebih kompleks, seperti aljabar dan kalkulus, serta memiliki aplikasi luas dalam kehidupan nyata.
Menunjukkan jumlah bagian
Dalam matematika, khususnya pada operasi pecahan, terdapat dua komponen penting yang disebut penyebut dan pembilang. Penyebut terletak di bagian bawah pecahan, sedangkan pembilang terletak di bagian atas. Salah satu peran penting dari penyebut adalah menunjukkan jumlah bagian yang sama dalam keseluruhan.
Sebagai contoh, pada pecahan 1/2, penyebutnya adalah 2. Ini berarti bahwa keseluruhan dibagi menjadi 2 bagian yang sama. Pembilangnya, yaitu 1, menunjukkan bahwa 1 dari 2 bagian tersebut diambil. Konsep ini sangat penting dalam memahami nilai dan operasi pecahan.
Dalam kehidupan nyata, konsep menunjukkan jumlah bagian ini juga memiliki aplikasi yang luas. Misalnya, dalam mengukur panjang menggunakan penggaris, penyebut menunjukkan jumlah bagian yang sama pada penggaris, seperti sentimeter atau inci. Pembilang menunjukkan banyaknya bagian tersebut yang diukur.
Dengan memahami konsep menunjukkan jumlah bagian pada penyebut, kita dapat lebih memahami nilai dan operasi pecahan, serta penerapannya dalam berbagai bidang, seperti pengukuran, pembagian, dan perbandingan nilai.
Menunjukkan banyaknya bagian
Dalam matematika, khususnya pada operasi pecahan, konsep “menunjukkan banyaknya bagian” sangat erat kaitannya dengan “penyebut” dan “pembilang”. Penyebut, yang terletak di bagian bawah pecahan, menunjukkan jumlah bagian yang sama dalam keseluruhan, sedangkan pembilang, yang terletak di bagian atas, menunjukkan banyaknya bagian tersebut yang diambil.
-
Peran dalam memahami nilai pecahan
Hubungan antara penyebut dan pembilang membantu kita memahami nilai pecahan. Penyebut menentukan ukuran setiap bagian, sedangkan pembilang menunjukkan berapa banyak bagian yang diambil. Dengan memahami hubungan ini, kita dapat membandingkan nilai pecahan yang berbeda secara akurat.
-
Aplikasi dalam kehidupan nyata
Konsep “menunjukkan banyaknya bagian” juga banyak digunakan dalam kehidupan nyata. Misalnya, dalam mengukur panjang menggunakan penggaris, penyebut menunjukkan jumlah bagian yang sama pada penggaris, seperti sentimeter atau inci, sedangkan pembilang menunjukkan berapa banyak bagian tersebut yang diukur. Hal ini membantu kita menentukan panjang suatu benda secara akurat.
-
Implikasi dalam operasi pecahan
Dalam operasi pecahan, seperti penjumlahan, pengurangan, perkalian, dan pembagian, memahami hubungan antara penyebut dan pembilang sangat penting. Misalnya, dalam penjumlahan pecahan, penyebut harus disamakan terlebih dahulu agar pecahan dapat dijumlahkan. Konsep “menunjukkan banyaknya bagian” membantu kita memahami mengapa langkah ini diperlukan.
Dengan memahami hubungan antara “menunjukkan banyaknya bagian” dengan “penyebut” dan “pembilang”, kita dapat lebih memahami nilai dan operasi pecahan, serta penerapannya dalam berbagai bidang, seperti pengukuran, perbandingan nilai, dan operasi matematika.
Penting untuk operasi pecahan
Dalam operasi pecahan, keberadaan penyebut dan pembilang sangatlah penting. Kedua komponen ini memainkan peran krusial dalam menentukan nilai dan operasi pecahan.
-
Peran dalam penjumlahan dan pengurangan
Dalam penjumlahan dan pengurangan pecahan, penyebut harus disamakan terlebih dahulu. Hal ini dimungkinkan karena penyebut menunjukkan jumlah bagian yang sama dalam keseluruhan. Dengan menyamakan penyebut, kita dapat menjumlahkan atau mengurangkan pembilang yang mewakili banyaknya bagian yang diambil.
-
Peran dalam perkalian dan pembagian
Dalam perkalian pecahan, penyebut dan pembilang dikalikan silang. Hal ini karena perkalian pecahan menunjukkan pengambilan bagian dari bagian. Demikian pula, dalam pembagian pecahan, pembilang dibalik dan dikalikan dengan pecahan yang lain. Operasi ini dimungkinkan karena penyebut dan pembilang menentukan ukuran dan banyaknya bagian pecahan.
-
Peran dalam mencari KPK dan FPB
Dalam operasi pecahan, seringkali diperlukan untuk mencari kelipatan persekutuan terkecil (KPK) atau faktor persekutuan terbesar (FPB) dari penyebut pecahan yang berbeda. Hal ini dimungkinkan karena penyebut menunjukkan jumlah bagian yang sama dalam keseluruhan. Dengan mengetahui KPK atau FPB, kita dapat melakukan operasi pecahan dengan lebih mudah dan akurat.
Dari uraian di atas, jelas terlihat bahwa penyebut dan pembilang memiliki peran yang sangat penting dalam operasi pecahan. Kedua komponen ini memungkinkan kita untuk melakukan berbagai operasi matematika pada pecahan, seperti penjumlahan, pengurangan, perkalian, pembagian, dan mencari KPK serta FPB.
Dasar matematika yang kompleks
Penyebut dan pembilang merupakan dasar bagi matematika yang lebih kompleks, seperti aljabar, kalkulus, dan trigonometri. Dalam aljabar, penyebut dan pembilang digunakan dalam penyederhanaan ekspresi aljabar, seperti pecahan aljabar dan persamaan rasional. Dalam kalkulus, konsep penyebut dan pembilang digunakan dalam turunan dan integral. Dalam trigonometri, penyebut dan pembilang digunakan dalam identitas trigonometri dan persamaan trigonometri.
Selain itu, pemahaman yang kuat tentang penyebut dan pembilang sangat penting untuk memahami konsep matematika yang lebih abstrak, seperti limit, deret tak hingga, dan fungsi kontinu. Konsep-konsep ini merupakan dasar bagi bidang matematika yang lebih tinggi, seperti analisis matematika dan topologi.
Dalam kehidupan nyata, pemahaman tentang penyebut dan pembilang sangat penting dalam berbagai aplikasi, seperti fisika, teknik, dan keuangan. Misalnya, dalam fisika, penyebut dan pembilang digunakan dalam menghitung kecepatan, percepatan, dan gaya. Dalam teknik, penyebut dan pembilang digunakan dalam menghitung tegangan, arus, dan hambatan listrik. Dalam keuangan, penyebut dan pembilang digunakan dalam menghitung bunga, laba, dan rugi.
Contoh
Contoh pecahan 1/2 dapat membantu kita memahami konsep penyebut dan pembilang dengan lebih jelas. Pada pecahan 1/2, angka 2 di bagian bawah disebut penyebut, yang menunjukkan bahwa keseluruhan dibagi menjadi 2 bagian yang sama. Angka 1 di bagian atas disebut pembilang, yang menunjukkan bahwa 1 dari 2 bagian tersebut diambil.
Dari contoh ini, kita dapat melihat bahwa penyebut dan pembilang bekerja sama untuk menentukan nilai pecahan. Penyebut menunjukkan ukuran setiap bagian, sedangkan pembilang menunjukkan banyaknya bagian yang diambil. Dengan memahami hubungan antara penyebut dan pembilang, kita dapat menghitung dan membandingkan nilai pecahan dengan lebih mudah.
Pemahaman tentang penyebut dan pembilang sangat penting dalam berbagai aplikasi kehidupan nyata. Misalnya, dalam mengukur panjang menggunakan penggaris, penyebut menunjukkan jumlah bagian yang sama pada penggaris, seperti sentimeter atau inci, sedangkan pembilang menunjukkan berapa banyak bagian tersebut yang diukur. Hal ini membantu kita menentukan panjang suatu benda secara akurat.
Pertanyaan Umum tentang Penyebut dan Pembilang
Bagian ini menyajikan beberapa pertanyaan umum dan jawabannya terkait dengan penyebut dan pembilang, dua komponen penting dalam matematika, khususnya pada operasi pecahan.
Pertanyaan 1: Apa yang dimaksud dengan penyebut dan pembilang?
Penyebut adalah bilangan di bagian bawah pecahan yang menunjukkan banyaknya bagian yang sama dalam keseluruhan. Pembilang adalah bilangan di bagian atas pecahan yang menunjukkan banyaknya bagian yang diambil dari keseluruhan.
Pertanyaan 2: Mengapa penyebut dan pembilang penting dalam operasi pecahan?
Penyebut dan pembilang sangat penting dalam operasi pecahan, seperti penjumlahan, pengurangan, perkalian, dan pembagian. Memahami konsep penyebut dan pembilang menjadi dasar bagi pemahaman matematika yang lebih kompleks.
Pertanyaan 3: Bagaimana cara mencari kelipatan persekutuan terkecil (KPK) dari penyebut pecahan yang berbeda?
Untuk mencari KPK dari penyebut pecahan yang berbeda, kita perlu mengalikan semua faktor prima dari setiap penyebut. Hasil perkalian tersebut adalah KPK dari penyebut-penyebut tersebut.
Pertanyaan 4: Apa saja aplikasi penyebut dan pembilang dalam kehidupan nyata?
Konsep penyebut dan pembilang memiliki banyak aplikasi dalam kehidupan nyata, seperti dalam mengukur panjang, berat, dan waktu, serta dalam bidang keuangan dan fisika.
Dengan memahami konsep penyebut dan pembilang, kita dapat memahami dan menggunakan pecahan dengan lebih efektif. Pecahan merupakan dasar dari banyak konsep matematika yang lebih kompleks, seperti aljabar dan kalkulus, serta memiliki aplikasi luas dalam kehidupan nyata.
Lanjut ke bagian Tips untuk mendapatkan informasi lebih lanjut tentang cara menggunakan penyebut dan pembilang secara efektif.
Tips Menggunakan Penyebut dan Pembilang Secara Efektif
Memahami konsep penyebut dan pembilang sangat penting untuk menguasai operasi pecahan dan matematika secara umum. Berikut adalah beberapa tips untuk menggunakan penyebut dan pembilang secara efektif:
Tip 1: Pahami konsep dasar penyebut dan pembilang
Penyebut menunjukkan jumlah bagian dalam keseluruhan, sedangkan pembilang menunjukkan banyaknya bagian yang diambil. Memahami konsep dasar ini akan membantu Anda memahami operasi pecahan.
Tip 2: Gunakan penyebut yang sama untuk menjumlahkan atau mengurangkan pecahan
Dalam penjumlahan atau pengurangan pecahan, penyebut harus disamakan terlebih dahulu. Ini dapat dilakukan dengan mencari kelipatan persekutuan terkecil (KPK) dari penyebut-penyebut tersebut.
Tip 3: Balikkan pecahan pembagi untuk melakukan pembagian
Saat membagi pecahan, pembilang dibalik dan dikalikan dengan pecahan yang lain. Operasi ini dikenal sebagai pembagian silang.
Tip 4: Gunakan penyederhanaan pecahan untuk mendapatkan pecahan yang lebih sederhana
Penyederhanaan pecahan dapat dilakukan dengan membagi pembilang dan penyebut dengan faktor persekutuan terbesar (FPB) mereka. Hal ini akan menghasilkan pecahan yang lebih sederhana dan mudah dioperasikan.
Dengan mengikuti tips ini, Anda dapat menggunakan penyebut dan pembilang secara efektif untuk menyelesaikan berbagai operasi pecahan dan masalah matematika lainnya.
Kesimpulannya, penyebut dan pembilang adalah komponen penting dalam matematika yang digunakan untuk merepresentasikan pecahan. Memahami konsep penyebut dan pembilang, serta cara menggunakannya secara efektif, akan membantu Anda menguasai matematika dan menyelesaikan masalah secara lebih efisien.
Kesimpulan
Penyebut dan pembilang merupakan konsep dasar dalam matematika yang digunakan untuk menyatakan pecahan. Memahami konsep dan operasi penyebut dan pembilang sangat penting untuk menguasai matematika dan menyelesaikan masalah secara efisien.
Dalam artikel ini, kita telah mengeksplorasi peran penting penyebut dan pembilang dalam operasi pecahan, seperti penjumlahan, pengurangan, perkalian, dan pembagian. Kita juga membahas pentingnya penyebut dan pembilang sebagai dasar untuk konsep matematika yang lebih kompleks, seperti aljabar dan kalkulus, serta aplikasinya dalam kehidupan nyata.
Memahami penyebut dan pembilang tidak hanya penting untuk kesuksesan akademis tetapi juga untuk kehidupan sehari-hari. Dari mengukur panjang hingga menghitung persentase, pemahaman yang kuat tentang penyebut dan pembilang sangat penting untuk menavigasi dunia di sekitar kita.



















