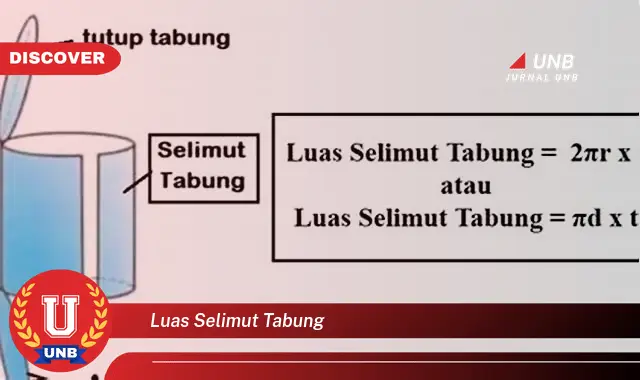
Luas selimut tabung adalah besaran yang menyatakan luas permukaan lengkung tabung. Luas selimut tabung dapat dihitung dengan menggunakan rumus 2r x t, di mana r adalah jari-jari alas atau tutup tabung dan t adalah tinggi tabung.
Luas selimut tabung memiliki beberapa manfaat dan peran penting. Beberapa di antaranya adalah:
- Dapat digunakan untuk menghitung volume tabung, karena luas selimut tabung merupakan bagian dari rumus volume tabung.
- Digunakan dalam berbagai bidang teknik dan industri, seperti perhitungan luas permukaan pipa, tangki, dan benda-benda berbentuk tabung lainnya.
- Memiliki nilai historis, karena konsep luas selimut tabung telah dikenal sejak zaman kuno dan digunakan dalam berbagai aplikasi matematika dan teknik.
Pada artikel ini, kita akan membahas lebih dalam tentang luas selimut tabung, termasuk rumus, sifat-sifat, dan penerapannya dalam berbagai bidang.
Luas Selimut Tabung
Luas selimut tabung merupakan aspek penting dalam memahami tabung dan aplikasinya. Berikut adalah 7 aspek penting terkait luas selimut tabung:
- Rumus
- Sifat
- Volume
- Teknik
- Industri
- Sejarah
- Aplikasi
Rumus luas selimut tabung, yaitu 2r x t, menjelaskan hubungan antara jari-jari alas/tutup (r) dan tinggi tabung (t). Sifat luas selimut tabung, seperti tidak bergantung pada jari-jari alas/tutup, memberikan pemahaman dasar tentang bentuk tabung. Luas selimut tabung juga berperan penting dalam menghitung volume tabung, yang merupakan besaran penting dalam berbagai bidang teknik dan industri.
Rumus
Rumus luas selimut tabung, yaitu 2r x t, memiliki peran penting dalam memahami luas selimut tabung. Rumus ini menjelaskan hubungan antara jari-jari alas/tutup (r) dan tinggi tabung (t). Dengan mengetahui rumus ini, kita dapat menghitung luas selimut tabung dengan mudah dan akurat.
Sebagai contoh, jika sebuah tabung memiliki jari-jari alas/tutup 5 cm dan tinggi 10 cm, maka luas selimut tabungnya adalah 2 x 5 cm x 10 cm = 100 cm. Pemahaman tentang rumus luas selimut tabung sangat bermanfaat, terutama dalam bidang teknik dan industri.
Dalam praktiknya, rumus luas selimut tabung digunakan untuk berbagai keperluan, seperti menghitung luas permukaan pipa, tangki, dan benda-benda berbentuk tabung lainnya. Dengan memahami rumus ini, kita dapat memperoleh informasi penting tentang luas permukaan benda-benda tersebut, yang sangat penting dalam perhitungan dan desain.
Sifat
Sifat luas selimut tabung memiliki peran penting dalam memahami karakteristik tabung secara keseluruhan. Berikut adalah beberapa sifat penting yang terkait dengan luas selimut tabung:
-
Tidak bergantung pada jari-jari alas/tutup
Luas selimut tabung tidak terpengaruh oleh jari-jari alas atau tutup tabung. Artinya, tabung dengan jari-jari alas/tutup berbeda tetapi memiliki tinggi yang sama akan memiliki luas selimut yang sama.
-
Proporsional dengan tinggi tabung
Luas selimut tabung berbanding lurus dengan tinggi tabung. Semakin tinggi tabung, semakin besar pula luas selimutnya.
-
Selalu berbentuk persegi panjang
Luas selimut tabung selalu berbentuk persegi panjang, dengan panjang sama dengan keliling alas atau tutup dan lebar sama dengan tinggi tabung.
-
Dapat dibagi menjadi dua bagian yang sama
Luas selimut tabung dapat dibagi menjadi dua bagian yang sama besar dengan bidang bagi yang sejajar dengan sumbu tabung.
Pemahaman tentang sifat-sifat luas selimut tabung ini sangat penting dalam berbagai aplikasi, seperti perhitungan volume tabung, luas permukaan benda-benda berbentuk tabung, dan desain benda-benda tersebut.
Volume
Volume tabung memiliki hubungan yang erat dengan luas selimut tabung. Volume tabung dapat dihitung dengan menggunakan rumus V = L x t, di mana L adalah luas selimut tabung dan t adalah tinggi tabung. Dengan demikian, luas selimut tabung merupakan komponen penting dalam menentukan volume tabung.
Sebagai contoh, sebuah tabung dengan jari-jari alas/tutup 5 cm dan tinggi 10 cm memiliki luas selimut 100 cm2. Volume tabung tersebut adalah 100 cm2 x 10 cm = 1000 cm3.
Pemahaman tentang hubungan antara luas selimut tabung dan volume tabung sangat penting dalam berbagai bidang, seperti teknik dan industri. Dalam teknik sipil, misalnya, perhitungan volume tabung digunakan untuk menentukan kapasitas tangki penyimpanan air atau bahan bakar. Dalam industri makanan, perhitungan volume tabung digunakan untuk menentukan isi kemasan makanan dan minuman berbentuk tabung, seperti kaleng dan botol.
Teknik
Dalam bidang teknik, luas selimut tabung memegang peranan penting dalam berbagai aspek, di antaranya:
-
Perhitungan Luas Permukaan
Luas selimut tabung digunakan untuk menghitung luas permukaan benda-benda berbentuk tabung, seperti pipa, tangki, dan tabung reaksi. Dengan mengetahui luas permukaan, insinyur dapat menentukan kebutuhan material, biaya pelapisan, dan aspek estetika.
-
Analisis Struktur
Luas selimut tabung juga berperan dalam analisis struktur tabung. Insinyur menggunakannya untuk menghitung tegangan dan regangan yang dialami tabung akibat beban yang diberikan. Hal ini penting untuk memastikan keamanan dan daya tahan struktur.
-
Desain dan Fabrikasi
Dalam desain dan fabrikasi, luas selimut tabung menjadi pertimbangan penting. Insinyur harus menentukan luas selimut tabung yang sesuai untuk memenuhi spesifikasi dan fungsi yang diinginkan, seperti kapasitas volume dan tekanan.
Dengan memahami peran luas selimut tabung dalam bidang teknik, insinyur dapat merancang dan membangun struktur dan sistem yang aman, efisien, dan efektif.
Industri
Luas selimut tabung memegang peranan penting dalam berbagai industri, di antaranya:
-
Industri Manufaktur
Dalam industri manufaktur, luas selimut tabung digunakan untuk menghitung luas permukaan benda-benda berbentuk tabung, seperti pipa, tabung reaksi, dan tangki penyimpanan. Perhitungan ini penting untuk menentukan kebutuhan bahan baku, biaya produksi, dan spesifikasi produk.
-
Industri Konstruksi
Pada industri konstruksi, luas selimut tabung digunakan untuk menghitung luas permukaan struktur berbentuk tabung, seperti pilar, kolom, dan pipa saluran. Perhitungan ini penting untuk menentukan kebutuhan material, seperti beton dan baja, serta untuk analisis struktur dan keamanan bangunan.
-
Industri Kemasan
Dalam industri kemasan, luas selimut tabung digunakan untuk menentukan ukuran dan bentuk kemasan produk yang berbentuk tabung, seperti kaleng, botol, dan tube pasta gigi. Perhitungan ini penting untuk memastikan produk dikemas dengan baik dan memenuhi standar kualitas.
-
Industri Otomotif
Pada industri otomotif, luas selimut tabung digunakan untuk menghitung luas permukaan komponen berbentuk tabung, seperti knalpot, pipa saluran bahan bakar, dan selang radiator. Perhitungan ini penting untuk menentukan kebutuhan material dan memastikan kinerja komponen yang optimal.
Dengan memahami peran luas selimut tabung dalam berbagai industri, pelaku usaha dapat mengoptimalkan proses produksi, desain produk, dan perhitungan biaya secara efisien dan akurat.
Sejarah
Sejarah memiliki kaitan erat dengan perkembangan konsep luas selimut tabung. Sejak zaman dahulu, tabung telah digunakan dalam berbagai aplikasi, seperti konstruksi, transportasi, dan penyimpanan. Dalam perjalanannya, pemahaman tentang luas selimut tabung terus berkembang, seiring dengan kebutuhan untuk menghitung luas permukaan dan volume tabung secara akurat.
Pada masa peradaban Mesir Kuno dan Babilonia, tabung telah banyak digunakan dalam sistem irigasi dan konstruksi bangunan. Meskipun konsep luas selimut tabung belum diformalkan pada waktu itu, para insinyur dan arsitek kuno telah menggunakan teknik empiris untuk memperkirakan luas permukaan tabung, sehingga memungkinkan mereka membangun struktur yang kokoh dan bertahan lama.
Perkembangan pesat dalam matematika dan geometri pada masa Yunani Kuno memberikan dasar teoretis untuk memahami luas selimut tabung. Matematikawan Yunani seperti Archimedes dan Euclid mengembangkan metode untuk menghitung luas dan volume bangun ruang, termasuk tabung. Mereka membuktikan rumus luas selimut tabung yang masih digunakan hingga saat ini, yaitu L = 2rh, di mana L adalah luas selimut tabung, adalah konstanta sekitar 3,14, r adalah jari-jari alas tabung, dan h adalah tinggi tabung.
Dalam perkembangan selanjutnya, konsep luas selimut tabung terus disempurnakan dan diterapkan pada berbagai bidang ilmu dan teknik. Pada abad ke-17, ilmuwan seperti Galileo Galilei dan Evangelista Torricelli menggunakan konsep luas selimut tabung dalam studi mereka tentang fluida dan tekanan udara. Pada abad ke-19, insinyur seperti James Watt dan George Stephenson memanfaatkan konsep ini dalam pengembangan mesin uap dan kereta api.
Hingga saat ini, luas selimut tabung tetap menjadi konsep dasar yang penting dalam berbagai bidang, seperti teknik sipil, teknik mesin, dan fisika. Pemahaman tentang luas selimut tabung sangat penting untuk merancang dan membangun struktur yang aman dan efisien, serta untuk menghitung volume dan luas permukaan benda-benda berbentuk tabung dalam berbagai aplikasi industri.
Aplikasi
Luas selimut tabung memiliki berbagai aplikasi penting dalam kehidupan sehari-hari dan berbagai bidang ilmu dan teknik. Pemahaman tentang luas selimut tabung sangat penting untuk menghitung luas permukaan dan volume benda-benda berbentuk tabung, sehingga memungkinkan kita untuk merancang, membangun, dan menganalisis berbagai struktur dan sistem dengan lebih akurat dan efisien.
Salah satu aplikasi penting luas selimut tabung adalah dalam perhitungan volume tabung. Volume tabung dapat dihitung dengan mengalikan luas selimut tabung dengan tinggi tabung. Aplikasi ini digunakan dalam berbagai bidang, seperti teknik sipil untuk menghitung volume tangki penyimpanan air, dan industri makanan untuk menghitung isi kemasan makanan dan minuman berbentuk tabung.
Selain itu, luas selimut tabung juga digunakan dalam analisis struktur. Dalam teknik sipil, luas selimut tabung digunakan untuk menghitung luas permukaan kolom dan pilar, yang penting untuk memastikan kekuatan dan stabilitas struktur bangunan. Dalam teknik mesin, luas selimut tabung digunakan untuk menghitung luas permukaan pipa dan tabung, yang penting untuk menganalisis aliran fluida dan perpindahan panas.
Dalam industri manufaktur, luas selimut tabung digunakan untuk menghitung luas permukaan benda-benda berbentuk tabung, seperti kaleng, pipa, dan tabung reaksi. Perhitungan ini penting untuk menentukan kebutuhan bahan baku, biaya produksi, dan spesifikasi produk.
Secara keseluruhan, pemahaman tentang luas selimut tabung memiliki aplikasi yang sangat luas dalam berbagai bidang, mulai dari teknik sipil dan mesin hingga industri manufaktur dan pengemasan. Dengan memahami konsep ini, kita dapat merancang, membangun, dan menganalisis struktur dan sistem yang lebih efisien, akurat, dan aman.
Pertanyaan Umum Seputar Luas Selimut Tabung
Bagian ini menyajikan beberapa pertanyaan umum beserta jawabannya seputar luas selimut tabung. Pemahaman yang baik terhadap konsep ini sangat penting dalam berbagai bidang teknik dan industri.
Pertanyaan 1: Apa itu luas selimut tabung?
Luas selimut tabung adalah besaran yang menyatakan luas permukaan lengkung tabung. Luas selimut tabung tidak termasuk luas permukaan alas dan tutup tabung.
Pertanyaan 2: Bagaimana cara menghitung luas selimut tabung?
Luas selimut tabung dapat dihitung menggunakan rumus L = 2r t, di mana L adalah luas selimut tabung, adalah konstanta sekitar 3,14, r adalah jari-jari alas atau tutup tabung, dan t adalah tinggi tabung.
Pertanyaan 3: Apa saja aplikasi luas selimut tabung?
Luas selimut tabung memiliki banyak aplikasi dalam berbagai bidang, seperti teknik sipil, teknik mesin, dan industri manufaktur. Beberapa aplikasinya termasuk menghitung volume tabung, luas permukaan benda-benda berbentuk tabung, dan analisis struktur.
Pertanyaan 4: Mengapa pemahaman tentang luas selimut tabung penting?
Pemahaman tentang luas selimut tabung sangat penting untuk merancang, membangun, dan menganalisis struktur dan sistem yang efisien dan aman. Konsep ini memungkinkan kita untuk menghitung luas permukaan dan volume benda-benda berbentuk tabung secara akurat, yang sangat penting dalam berbagai aplikasi teknik dan industri.
Dengan memahami konsep luas selimut tabung dan aplikasinya, kita dapat berkontribusi pada pengembangan struktur dan sistem yang lebih baik dan inovatif di berbagai bidang.
Selanjutnya, mari kita bahas beberapa tips untuk menghitung dan menerapkan luas selimut tabung secara efektif dalam praktik.
Tips Menghitung dan Menerapkan Luas Selimut Tabung
Untuk menghitung dan menerapkan luas selimut tabung secara efektif, berikut adalah beberapa tips yang dapat diikuti:
Tips 1: Pahami Konsep Dasar
Sebelum melakukan perhitungan, pastikan untuk memahami konsep dasar luas selimut tabung, termasuk rumus dan sifat-sifatnya. Pemahaman yang kuat akan memudahkan proses perhitungan dan penerapan.
Tips 2: Gunakan Rumus yang Tepat
Gunakan rumus luas selimut tabung yang sesuai dengan bentuk dan ukuran tabung. Pastikan untuk menggunakan nilai jari-jari dan tinggi tabung yang benar untuk mendapatkan hasil yang akurat.
Tips 3: Perhatikan Satuan
Perhatikan satuan yang digunakan dalam perhitungan luas selimut tabung. Konsistensi satuan sangat penting untuk memastikan hasil yang bermakna dan menghindari kesalahan.
Tips 4: Terapkan dalam Konteks Praktis
Setelah menghitung luas selimut tabung, terapkan hasilnya secara tepat dalam konteks praktis. Misalnya, untuk menghitung volume tabung atau luas permukaan benda-benda berbentuk tabung.
Dengan mengikuti tips ini, kita dapat menghitung dan menerapkan luas selimut tabung secara akurat dan efektif dalam berbagai aplikasi teknik dan industri.
Selanjutnya, mari kita bahas kesimpulan dari pembahasan kita tentang luas selimut tabung dan aplikasinya.
Kesimpulan
Luas selimut tabung merupakan besaran penting yang memiliki berbagai aplikasi dalam bidang teknik dan industri. Pemahaman tentang luas selimut tabung sangat penting untuk menghitung luas permukaan dan volume tabung secara akurat, sehingga memungkinkan kita untuk merancang, membangun, dan menganalisis struktur dan sistem yang efisien dan aman.
Dalam artikel ini, kita telah membahas secara mendalam tentang luas selimut tabung, termasuk rumus, sifat, volume, teknik, industri, sejarah, dan aplikasinya. Dengan memahami konsep ini dan menerapkannya secara efektif, kita dapat berkontribusi pada pengembangan struktur dan sistem yang lebih baik dan inovatif di berbagai bidang.