Besaran turunan adalah besaran yang diturunkan dari besaran pokok. Besaran pokok adalah besaran yang tidak dapat diturunkan dari besaran lain, seperti panjang, massa, waktu, suhu, dan kuat arus listrik.
Sementara itu, besaran turunan adalah besaran yang dapat diturunkan dari besaran pokok, seperti luas, volume, kecepatan, percepatan, dan gaya.
Besaran turunan sangat penting dalam sains karena memungkinkan kita untuk mengukur dan menghitung besaran yang tidak dapat diukur secara langsung.
Misalnya, kita tidak dapat mengukur kecepatan secara langsung, tetapi kita dapat menghitungnya dengan membagi jarak yang ditempuh dengan waktu yang dibutuhkan untuk menempuh jarak tersebut.
Demikian pula, kita tidak dapat mengukur percepatan secara langsung, tetapi kita dapat menghitungnya dengan membagi perubahan kecepatan dengan waktu yang dibutuhkan untuk perubahan tersebut.
Besaran turunan telah digunakan selama berabad-abad untuk mengukur dan menghitung dunia di sekitar kita. Fisikawan awal seperti Galileo dan Newton menggunakan besaran turunan untuk mengembangkan hukum gerak dan gravitasi.
Saat ini, besaran turunan digunakan di semua bidang sains dan teknik untuk mengukur dan menghitung segala sesuatu mulai dari gerakan benda hingga sifat bahan.
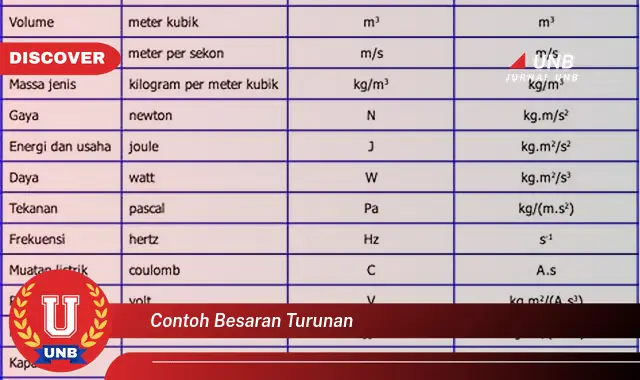
Contoh Besaran Turunan
Besaran turunan merupakan besaran yang diturunkan dari besaran pokok. Besaran pokok adalah besaran yang tidak dapat diturunkan dari besaran lain, seperti panjang, massa, waktu, suhu, dan kuat arus listrik.
Sementara itu, besaran turunan adalah besaran yang dapat diturunkan dari besaran pokok, seperti luas, volume, kecepatan, percepatan, dan gaya.
- Luas
- Volume
- Kecepatan
- Percepatan
- Gaya
- Energi
- Daya
Besaran turunan sangat penting dalam sains karena memungkinkan kita untuk mengukur dan menghitung besaran yang tidak dapat diukur secara langsung.
Misalnya, kita tidak dapat mengukur kecepatan secara langsung, tetapi kita dapat menghitungnya dengan membagi jarak yang ditempuh dengan waktu yang dibutuhkan untuk menempuh jarak tersebut.
Demikian pula, kita tidak dapat mengukur percepatan secara langsung, tetapi kita dapat menghitungnya dengan membagi perubahan kecepatan dengan waktu yang dibutuhkan untuk perubahan tersebut.
Besaran turunan telah digunakan selama berabad-abad untuk mengukur dan menghitung dunia di sekitar kita. Fisikawan awal seperti Galileo dan Newton menggunakan besaran turunan untuk mengembangkan hukum gerak dan gravitasi.
Saat ini, besaran turunan digunakan di semua bidang sains dan teknik untuk mengukur dan menghitung segala sesuatu mulai dari gerakan benda hingga sifat bahan.
Luas
Luas adalah besaran turunan yang digunakan untuk mengukur ukuran suatu permukaan. Luas dapat dinyatakan dalam satuan meter persegi (m), sentimeter persegi (cm), atau kilometer persegi (km).
-
Menghitung luas
Luas dapat dihitung dengan mengalikan panjang dan lebar suatu permukaan. Misalnya, jika sebuah persegi panjang memiliki panjang 5 cm dan lebar 3 cm, maka luasnya adalah 5 cm x 3 cm = 15 cm. -
Jenis-jenis luas
Ada berbagai jenis luas, antara lain luas persegi, luas persegi panjang, luas segitiga, dan luas lingkaran. Setiap jenis luas memiliki rumus yang berbeda untuk menghitungnya. -
Penerapan luas
Luas memiliki banyak penerapan dalam kehidupan sehari-hari, misalnya untuk menghitung luas tanah, luas bangunan, atau luas suatu bidang dalam gambar teknik.
Luas merupakan besaran turunan yang penting karena memungkinkan kita untuk mengukur ukuran suatu permukaan. Luas digunakan dalam berbagai bidang, seperti arsitektur, teknik sipil, dan pertanian.
Volume
Volume adalah besaran turunan yang digunakan untuk mengukur ukuran ruang tiga dimensi. Volume dapat dinyatakan dalam satuan meter kubik (m3), sentimeter kubik (cm3), atau liter (L).
-
Menghitung volume
Volume dapat dihitung dengan mengalikan panjang, lebar, dan tinggi suatu benda. Misalnya, jika sebuah balok memiliki panjang 5 cm, lebar 3 cm, dan tinggi 2 cm, maka volumenya adalah 5 cm x 3 cm x 2 cm = 30 cm3. -
Jenis-jenis volume
Ada berbagai jenis volume, antara lain volume kubus, volume balok, volume prisma, dan volume kerucut. Setiap jenis volume memiliki rumus yang berbeda untuk menghitungnya. -
Penerapan volume
Volume memiliki banyak penerapan dalam kehidupan sehari-hari, misalnya untuk menghitung volume air dalam suatu wadah, volume tanah dalam suatu galian, atau volume suatu benda dalam gambar teknik.
Volume merupakan besaran turunan yang penting karena memungkinkan kita untuk mengukur ukuran ruang tiga dimensi. Volume digunakan dalam berbagai bidang, seperti fisika, kimia, dan teknik sipil.
Kecepatan
Kecepatan adalah besaran turunan yang digunakan untuk mengukur seberapa cepat suatu benda bergerak. Kecepatan dapat dinyatakan dalam satuan meter per sekon (m/s), kilometer per jam (km/jam), atau mil per jam (mph).
-
Definisi Kecepatan
Kecepatan didefinisikan sebagai jarak yang ditempuh oleh suatu benda per satuan waktu. Jarak diukur dalam meter (m), dan waktu diukur dalam sekon (s). Jadi, satuan kecepatan adalah meter per sekon (m/s). -
Jenis-jenis Kecepatan
Ada dua jenis kecepatan, yaitu kecepatan rata-rata dan kecepatan sesaat. Kecepatan rata-rata adalah kecepatan benda selama selang waktu tertentu, sedangkan kecepatan sesaat adalah kecepatan benda pada suatu saat tertentu. -
Penerapan Kecepatan
Kecepatan memiliki banyak penerapan dalam kehidupan sehari-hari, misalnya untuk mengukur kecepatan kendaraan, kecepatan aliran air, atau kecepatan suatu reaksi kimia.
Kecepatan merupakan besaran turunan yang penting karena memungkinkan kita untuk mengukur seberapa cepat suatu benda bergerak. Kecepatan digunakan dalam berbagai bidang, seperti fisika, teknik, dan transportasi.
Percepatan
Percepatan adalah besaran turunan yang mengukur seberapa cepat suatu benda bergerak dalam arah tertentu. Percepatan didefinisikan sebagai perubahan kecepatan benda per satuan waktu. Satuan percepatan adalah meter per sekon kuadrat (m/s).
Percepatan merupakan besaran turunan yang penting karena memungkinkan kita untuk mengukur perubahan kecepatan suatu benda. Percepatan digunakan dalam berbagai bidang, seperti fisika, teknik, dan transportasi.
Contoh penerapan percepatan dalam kehidupan sehari-hari antara lain:
- Percepatan mobil yang sedang melaju
- Percepatan gravitasi bumi yang menyebabkan benda jatuh
- Percepatan suatu roket yang sedang lepas landas
Memahami konsep percepatan sangat penting untuk memahami dinamika benda dan gaya yang bekerja padanya.
Gaya
Gaya merupakan besaran turunan yang penting dalam fisika. Gaya didefinisikan sebagai tarikan atau dorongan yang bekerja pada suatu benda, yang dapat mengubah kecepatan atau arah geraknya. Satuan gaya adalah Newton (N).
-
Jenis-jenis Gaya
– Gaya Gravitasi: Gaya tarik-menarik antara dua benda yang memiliki massa.
– Gaya Gesek: Gaya yang timbul akibat adanya permukaan yang saling bersentuhan.
– Gaya Elektromagnetik: Gaya yang timbul akibat adanya muatan listrik dan magnet.
– Gaya Pegas: Gaya yang timbul akibat adanya pegas yang diregangkan atau dikompresi. -
Penerapan Gaya
Gaya memiliki banyak penerapan dalam kehidupan sehari-hari, seperti:
– Gaya yang digunakan untuk mendorong atau menarik benda.
– Gaya yang digunakan untuk mengangkat beban.
– Gaya yang digunakan untuk menggerakkan kendaraan.
Dalam konteks contoh besaran turunan, gaya merupakan besaran yang dapat diturunkan dari besaran pokok massa, panjang, dan waktu. Gaya dapat digunakan untuk menghitung besaran turunan lainnya, seperti usaha, energi, dan momentum.
Energi
Energi merupakan besaran turunan yang penting dalam fisika. Energi didefinisikan sebagai kemampuan suatu benda untuk melakukan usaha. Satuan energi adalah Joule (J).
-
Jenis-jenis Energi
– Energi Kinetik: Energi yang dimiliki suatu benda karena geraknya.
– Energi Potensial: Energi yang dimiliki suatu benda karena posisinya.
– Energi Listrik: Energi yang dimiliki suatu benda karena muatan listriknya.
– Energi Panas: Energi yang dimiliki suatu benda karena suhunya. -
Penerapan Energi
Energi memiliki banyak penerapan dalam kehidupan sehari-hari, seperti:
– Energi yang digunakan untuk menggerakkan kendaraan.
– Energi yang digunakan untuk menghasilkan listrik.
– Energi yang digunakan untuk memanaskan makanan. -
Energi dalam Konteks Contoh Besaran Turunan
Energi merupakan besaran yang dapat diturunkan dari besaran pokok massa, panjang, dan waktu. Energi dapat digunakan untuk menghitung besaran turunan lainnya, seperti usaha, gaya, dan momentum.
Energi merupakan besaran turunan yang sangat penting dalam fisika karena memungkinkan kita untuk memahami dan menghitung perubahan yang terjadi pada benda-benda di sekitar kita.
Energi memiliki banyak penerapan dalam kehidupan sehari-hari, mulai dari menggerakkan kendaraan hingga menghasilkan listrik.
Daya
Daya merupakan besaran turunan yang penting dalam fisika karena memungkinkan kita untuk mengukur laju di mana usaha dilakukan atau energi dipindahkan. Daya didefinisikan sebagai usaha yang dilakukan atau energi yang dipindahkan per satuan waktu.
Satuan daya adalah Watt (W).
-
Peran Daya dalam Contoh Besaran Turunan
Daya dapat digunakan untuk menghitung besaran turunan lainnya, seperti usaha dan energi.
Misalnya, kita dapat menghitung usaha yang dilakukan oleh gaya dengan mengalikan gaya dengan jarak yang dipindahkan dan waktu yang dibutuhkan untuk memindahkan jarak tersebut.
Kita juga dapat menghitung energi yang dipindahkan oleh daya dengan mengalikan daya dengan waktu.
-
Contoh Daya dalam Kehidupan Sehari-hari
Daya memiliki banyak penerapan dalam kehidupan sehari-hari, seperti:
- Daya yang digunakan oleh peralatan listrik, seperti lampu, kipas angin, dan AC.
- Daya yang dihasilkan oleh mesin, seperti mesin kendaraan dan mesin industri.
- Daya yang digunakan oleh manusia untuk melakukan aktivitas sehari-hari, seperti berjalan, berlari, dan mengangkat beban.
-
Implikasi Daya dalam Contoh Besaran Turunan
Daya merupakan besaran yang penting untuk dipertimbangkan dalam merancang dan mengoperasikan sistem dan mesin. Misalnya, dalam merancang sistem kelistrikan, kita perlu mempertimbangkan daya yang dibutuhkan oleh peralatan listrik dan memilih sumber daya yang sesuai.
Demikian pula, dalam mengoperasikan mesin, kita perlu mempertimbangkan daya yang dihasilkan oleh mesin dan memastikan bahwa daya tersebut cukup untuk menjalankan beban yang diberikan.
Daya merupakan besaran turunan yang sangat penting dalam fisika dan teknik. Daya memungkinkan kita untuk mengukur laju di mana usaha dilakukan atau energi dipindahkan, dan memiliki banyak penerapan dalam kehidupan sehari-hari.
Berikut ini adalah beberapa pertanyaan umum yang sering diajukan tentang besaran turunan, beserta jawabannya.
Pertanyaan 1: Apa yang dimaksud dengan besaran turunan?
Besaran turunan adalah besaran yang diturunkan dari besaran pokok. Besaran pokok adalah besaran yang tidak dapat diturunkan dari besaran lain, seperti panjang, massa, waktu, suhu, dan kuat arus listrik.
Pertanyaan 2: Apa saja contoh besaran turunan?
Contoh besaran turunan antara lain luas, volume, kecepatan, percepatan, gaya, energi, dan daya.
Pertanyaan 3: Apa pentingnya besaran turunan?
Besaran turunan sangat penting dalam sains karena memungkinkan kita untuk mengukur dan menghitung besaran yang tidak dapat diukur secara langsung.
Misalnya, kita tidak dapat mengukur kecepatan secara langsung, tetapi kita dapat menghitungnya dengan membagi jarak yang ditempuh dengan waktu yang dibutuhkan untuk menempuh jarak tersebut.
Pertanyaan 4: Apa saja penerapan besaran turunan?
Besaran turunan memiliki banyak penerapan dalam kehidupan sehari-hari, seperti untuk mengukur luas tanah, volume air dalam suatu wadah, kecepatan kendaraan, dan gaya yang bekerja pada suatu benda.
Kesimpulannya, besaran turunan merupakan konsep penting dalam sains yang memungkinkan kita untuk mengukur dan menghitung berbagai besaran yang tidak dapat diukur secara langsung.
Besaran turunan memiliki banyak penerapan dalam berbagai bidang, seperti fisika, teknik, dan kehidupan sehari-hari.
Selanjutnya, kita akan membahas beberapa tips untuk memahami dan menggunakan besaran turunan dalam perhitungan fisika.
Berikut ini beberapa tips yang dapat membantu Anda dalam memahami dan menggunakan besaran turunan:
Tip 1: Kenali besaran pokok dan besaran turunan
Memahami perbedaan antara besaran pokok dan besaran turunan sangat penting. Besaran pokok adalah besaran yang tidak dapat diturunkan dari besaran lain, seperti panjang, massa, waktu, suhu, dan kuat arus listrik.
Sementara itu, besaran turunan adalah besaran yang diturunkan dari besaran pokok, seperti luas, volume, kecepatan, percepatan, gaya, energi, dan daya.
Tip 2: Pelajari rumus dan satuan besaran turunan
Setiap besaran turunan memiliki rumus dan satuan yang berbeda. Penting untuk mempelajari rumus dan satuan ini untuk dapat menghitung dan menggunakan besaran turunan dengan benar.
Misalnya, rumus luas persegi adalah panjang x lebar, dan satuan luas adalah meter persegi.
Tip 3: Perhatikan dimensi besaran turunan
Dimensi besaran turunan menunjukkan besaran pokok yang terkandung dalam besaran turunan tersebut. Dimensi besaran turunan dapat digunakan untuk memeriksa kebenaran perhitungan dan persamaan. Misalnya, dimensi kecepatan adalah panjang dibagi waktu, atau L/T.
Tip 4: Terapkan besaran turunan dalam konteks
Besaran turunan memiliki banyak penerapan dalam kehidupan sehari-hari. Cobalah untuk menerapkan besaran turunan dalam konteks yang relevan untuk memperkuat pemahaman Anda.
Misalnya, Anda dapat menghitung luas ruangan untuk menentukan jumlah cat yang dibutuhkan, atau menghitung kecepatan kendaraan untuk mengetahui waktu tempuh perjalanan.
Besaran turunan merupakan besaran yang sangat penting dalam sains dan teknik. Besaran turunan memungkinkan kita untuk mengukur dan menghitung besaran yang tidak dapat diukur secara langsung.
Berbagai besaran turunan, seperti luas, volume, kecepatan, percepatan, gaya, energi, dan daya, memiliki rumus dan satuan yang berbeda-beda.
Memahami konsep besaran turunan dan cara menggunakannya sangat penting untuk menyelesaikan masalah dan membuat prediksi dalam berbagai bidang sains dan teknik.
Di masa depan, diharapkan penelitian dan pengembangan di bidang besaran turunan terus berkembang.
Hal ini akan memungkinkan kita untuk mengukur dan menghitung besaran yang lebih kompleks dan akurat, sehingga dapat memberikan kontribusi yang lebih besar bagi kemajuan ilmu pengetahuan dan teknologi.



















