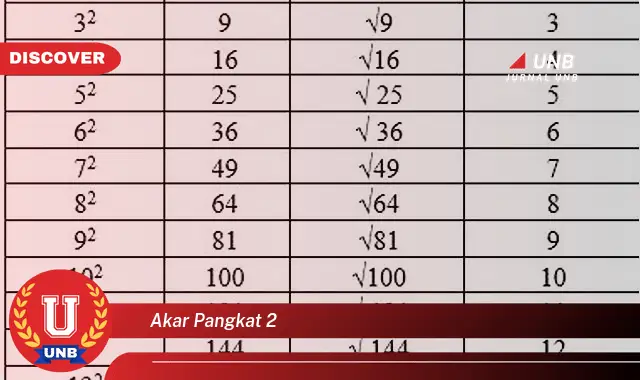
Akar pangkat 2, juga dikenal sebagai akar kuadrat, adalah operasi matematika yang digunakan untuk mencari nilai yang jika dikuadratkan akan menghasilkan angka tertentu. Dalam istilah yang lebih sederhana, akar pangkat 2 adalah bilangan yang, jika dikalikan dengan dirinya sendiri, menghasilkan bilangan asli. Misalnya, akar pangkat 2 dari 9 adalah 3, karena 3 x 3 = 9.
Operasi akar pangkat 2 sangat penting dalam berbagai bidang, termasuk matematika, fisika, dan teknik. Ini digunakan untuk memecahkan persamaan kuadrat, menghitung jarak dan luas, dan memahami konsep-konsep ilmiah seperti percepatan dan energi. Selain itu, akar pangkat 2 memiliki sejarah panjang, yang berasal dari zaman Babilonia kuno.
Dalam artikel ini, kita akan membahas pentingnya akar pangkat 2, manfaatnya, dan konteks sejarahnya. Kami juga akan mengeksplorasi beberapa aplikasi umum akar pangkat 2 dalam kehidupan sehari-hari.
akar pangkat 2
Akar pangkat 2, atau akar kuadrat, adalah konsep matematika yang penting dengan berbagai aplikasi. Berikut adalah tujuh aspek penting yang berkaitan dengan akar pangkat 2:
- Definisi
- Operasi
- Sifat
- Aplikasi
- Sejarah
- Contoh
- Kaitan dengan topik lain
Definisi akar pangkat 2 adalah bilangan yang, jika dikuadratkan, menghasilkan bilangan tertentu. Operasi akar pangkat 2 dilambangkan dengan tanda . Sifat-sifat akar pangkat 2 meliputi fakta bahwa akar pangkat 2 dari hasil kali dua bilangan sama dengan hasil kali akar pangkat 2 dari kedua bilangan tersebut. Akar pangkat 2 juga memiliki banyak aplikasi, termasuk menyelesaikan persamaan kuadrat dan menghitung jarak. Akar pangkat 2 memiliki sejarah panjang, yang berasal dari zaman Babilonia kuno. Contoh akar pangkat 2 termasuk 9 = 3 dan 16 = 4. Akar pangkat 2 juga terkait dengan topik lain dalam matematika, seperti aljabar dan geometri.
Definisi
Definisi akar pangkat 2 adalah konsep dasar yang menjadi landasan semua operasi dan aplikasi terkait. Definisi ini memberikan pemahaman yang jelas tentang sifat fundamental akar pangkat 2 dan perannya dalam matematika.
-
Akar pangkat 2 sebagai bilangan yang dikuadratkan
Definisi akar pangkat 2 sebagai bilangan yang, jika dikuadratkan, menghasilkan bilangan tertentu sangat penting. Definisi ini membentuk dasar untuk memahami operasi dan sifat akar pangkat 2. Sebagai contoh, akar pangkat 2 dari 9 adalah 3 karena 3 x 3 = 9.
-
Notasi akar pangkat 2
Notasi akar pangkat 2, yang dilambangkan dengan tanda , adalah aspek penting dari definisinya. Notasi ini memungkinkan kita untuk secara jelas menyatakan operasi akar pangkat 2 dan membedakannya dari operasi matematika lainnya. Misalnya, 9 menunjukkan akar pangkat 2 dari 9.
-
Akar pangkat 2 bilangan positif dan negatif
Definisi akar pangkat 2 juga berlaku untuk bilangan positif dan negatif. Untuk bilangan positif, akar pangkat 2 selalu positif. Namun, untuk bilangan negatif, akar pangkat 2 tidak didefinisikan dalam bilangan real. Konsep bilangan kompleks diperkenalkan untuk memperluas definisi akar pangkat 2 ke bilangan negatif.
-
Sifat dasar akar pangkat 2
Definisi akar pangkat 2 mengarah pada sifat dasar tertentu, seperti fakta bahwa akar pangkat 2 dari hasil kali dua bilangan sama dengan hasil kali akar pangkat 2 dari kedua bilangan tersebut. Sifat-sifat ini sangat penting untuk memanipulasi dan menyelesaikan persamaan yang melibatkan akar pangkat 2.
Dengan memahami definisi akar pangkat 2, kita dapat membangun dasar yang kuat untuk mengeksplorasi operasi, sifat, dan aplikasi yang lebih kompleks dari konsep matematika yang penting ini.
Operasi
Operasi yang melibatkan akar pangkat 2 sangat penting untuk memanipulasi dan menyelesaikan persamaan yang mengandungnya. Beberapa operasi umum yang terkait dengan akar pangkat 2 meliputi:
-
Menghitung akar pangkat 2
Operasi paling dasar adalah menghitung akar pangkat 2 dari suatu bilangan. Operasi ini dilakukan dengan mencari bilangan yang, jika dikuadratkan, menghasilkan bilangan asli. Misalnya, akar pangkat 2 dari 9 adalah 3 karena 3 x 3 = 9.
-
Menjumlahkan dan mengurangkan akar pangkat 2
Akar pangkat 2 dari bilangan yang berbeda dapat dijumlahkan atau dikurangkan, selama bilangan di bawah tanda akar pangkat adalah bilangan rasional sempurna. Misalnya, 3 + 4 = 7.
-
Mengalikan dan membagi akar pangkat 2
Akar pangkat 2 dari bilangan yang berbeda dapat dikalikan atau dibagi. Aturan dasar untuk operasi ini adalah mengalikan atau membagi bilangan di bawah tanda akar pangkat. Misalnya, 3 x 4 = 12 dan 6 2 = 3.
-
Menerapkan sifat-sifat akar pangkat 2
Beberapa sifat akar pangkat 2, seperti sifat distributif dan asosiatif, dapat digunakan untuk menyederhanakan operasi yang melibatkan akar pangkat 2. Misalnya, 3 x ( 2 + 3) = 32 + 33.
Pemahaman operasi yang melibatkan akar pangkat 2 sangat penting untuk menyelesaikan berbagai masalah matematika, termasuk menyelesaikan persamaan kuadrat, menghitung jarak, dan memahami konsep fisika seperti percepatan dan energi.
Sifat
Sifat-sifat akar pangkat dua sangat penting dalam memahami dan memanipulasi operasi yang melibatkannya. Sifat-sifat ini menentukan perilaku akar pangkat dua dalam berbagai operasi matematika, sehingga memudahkan kita untuk menyelesaikan persamaan, menyederhanakan ekspresi, dan memahami konsep matematika yang lebih kompleks.
Salah satu sifat penting dari akar pangkat dua adalah sifat distributif, yang menyatakan bahwa akar pangkat dua dari jumlah dua bilangan kuadrat sama dengan akar pangkat dua dari masing-masing bilangan tersebut dijumlahkan. Sifat ini sangat berguna dalam menyederhanakan ekspresi yang melibatkan akar pangkat dua.
Selain itu, akar pangkat dua juga memiliki sifat asosiatif, yang menyatakan bahwa akar pangkat dua dari hasil kali dua bilangan kuadrat sama dengan hasil kali akar pangkat dua dari masing-masing bilangan tersebut. Sifat ini memungkinkan kita untuk mengelompokkan bilangan di bawah akar pangkat dua dengan cara yang lebih fleksibel.
Sifat-sifat akar pangkat dua lainnya termasuk sifat identitas, yang menyatakan bahwa akar pangkat dua dari suatu bilangan kuadrat adalah bilangan itu sendiri, dan sifat invers, yang menyatakan bahwa akar pangkat dua dari hasil bagi dua bilangan kuadrat sama dengan hasil bagi akar pangkat dua dari masing-masing bilangan tersebut.
Memahami sifat-sifat akar pangkat dua sangat penting untuk membangun fondasi yang kuat dalam matematika dan untuk dapat menyelesaikan masalah matematika yang lebih kompleks secara efektif.
Aplikasi
Akar pangkat 2 memiliki beragam aplikasi dalam berbagai bidang, termasuk matematika, fisika, dan teknik. Salah satu aplikasi pentingnya adalah dalam menyelesaikan persamaan kuadrat, yang merupakan persamaan yang berbentuk ax^2 + bx + c = 0. Akar pangkat 2 digunakan untuk menemukan nilai x yang memenuhi persamaan tersebut.
Selain itu, akar pangkat 2 juga digunakan dalam menghitung jarak dan luas. Misalnya, dalam menghitung jarak antara dua titik (x1, y1) dan (x2, y2), digunakan rumus jarak = [(x2 – x1)^2 + (y2 – y1)^2]. Rumus ini melibatkan operasi akar pangkat 2 untuk menentukan jarak antara kedua titik tersebut.
Dalam fisika, akar pangkat 2 digunakan dalam konsep percepatan dan energi. Misalnya, dalam persamaan gerak v^2 = u^2 + 2as, akar pangkat 2 digunakan untuk menghitung kecepatan akhir (v) suatu benda berdasarkan kecepatan awalnya (u), percepatan (a), dan jarak yang ditempuh (s). Demikian pula, dalam persamaan energi kinetik Ek = 1/2mv^2, akar pangkat 2 digunakan untuk menghitung energi kinetik suatu benda berdasarkan massanya (m) dan kecepatannya (v).
Pemahaman tentang aplikasi akar pangkat 2 sangat penting untuk memahami berbagai konsep matematika dan fisika, serta untuk menyelesaikan masalah praktis dalam kehidupan sehari-hari.
Sejarah
Sejarah memainkan peran krusial dalam perkembangan konsep akar pangkat 2. Pemahaman tentang akar pangkat 2 telah berevolusi seiring waktu, berkontribusi pada kemajuan matematika dan bidang terkait lainnya.
-
Asal-Usul Kuno
Konsep akar pangkat 2 dapat ditelusuri kembali ke zaman Babilonia kuno. Bangsa Babilonia menggunakan tabel matematika untuk menghitung akar pangkat 2, yang menunjukkan bahwa mereka memiliki pemahaman dasar tentang operasi ini.
-
Perkembangan di Yunani Kuno
Matematikawan Yunani, seperti Pythagoras dan Euclid, memberikan kontribusi signifikan terhadap pengembangan akar pangkat 2. Pythagoras menemukan hubungan antara akar pangkat 2 dan geometri, sedangkan Euclid memberikan bukti formal untuk sifat-sifat akar pangkat 2.
-
Masa Renaisans dan Abad Pertengahan
Selama masa Renaisans dan Abad Pertengahan, para matematikawan melanjutkan studi mereka tentang akar pangkat 2. Fibonacci mengembangkan metode untuk memperkirakan akar pangkat 2 menggunakan deret, sementara al-Khwarizmi memperkenalkan konsep bilangan kompleks, yang memperluas definisi akar pangkat 2 ke bilangan negatif.
-
Era Modern
Pada era modern, perkembangan kalkulus dan aljabar abstrak semakin memperluas pemahaman kita tentang akar pangkat 2. Akar pangkat 2 sekarang digunakan secara luas dalam berbagai bidang, termasuk matematika murni, fisika, dan teknik.
Memahami sejarah akar pangkat 2 memberikan apresiasi terhadap perkembangan konsep matematika yang penting ini. Ini menyoroti kontribusi para matematikawan dari berbagai era dan budaya, yang telah membentuk pemahaman kita tentang akar pangkat 2 dan aplikasinya.
Contoh
Contoh memainkan peran penting dalam memahami konsep akar pangkat 2 secara konkret. Dengan mengeksplorasi contoh-contoh praktis, kita dapat memvisualisasikan operasi dan aplikasi akar pangkat 2, sehingga memudahkan pemahaman dan penerapannya.
-
Menghitung Panjang Diagonal Persegi
Akar pangkat 2 digunakan untuk menghitung panjang diagonal persegi. Jika sisi persegi memiliki panjang “s”, maka panjang diagonalnya adalah s2. Contohnya, jika sisi persegi adalah 5 cm, maka panjang diagonalnya adalah 52 cm 7,07 cm.
-
Menghitung Kecepatan Rata-Rata
Akar pangkat 2 juga digunakan dalam menghitung kecepatan rata-rata. Jika jarak yang ditempuh adalah “d” dan waktu yang diperlukan adalah “t”, maka kecepatan rata-rata adalah d/t2. Contohnya, jika jarak yang ditempuh adalah 100 km dan waktu yang diperlukan adalah 1 jam, maka kecepatan rata-rata adalah 100 km/jam 2 70,71 km/jam.
-
Menghitung Volume Kubus
Akar pangkat 2 digunakan untuk menghitung volume kubus. Jika panjang rusuk kubus adalah “a”, maka volumenya adalah a2. Misalnya, jika panjang rusuk kubus adalah 3 cm, maka volumenya adalah 3 cm2 10,39 cm.
-
Menghitung Periode Gerak Harmonik Sederhana
Akar pangkat 2 digunakan dalam menghitung periode gerak harmonik sederhana. Jika massa benda adalah “m”, konstanta pegas adalah “k”, dan amplitudo gerak adalah “A”, maka periodenya adalah 2m/k. Contohnya, jika massa benda adalah 0,5 kg, konstanta pegas adalah 10 N/m, dan amplitudo gerak adalah 0,1 m, maka periodenya adalah 20,5 kg/10 N/m 2,83 s.
Contoh-contoh ini menunjukkan aplikasi nyata akar pangkat 2 dalam berbagai bidang, sehingga memperkuat pemahaman kita tentang konsep penting ini.
Kaitan dengan Topik Lain
Akar pangkat dua memiliki keterkaitan yang erat dengan berbagai topik lain dalam matematika dan bidang terkait, yang memperluas aplikasi dan pemahaman konsep penting ini.
-
Aljabar
Akar pangkat dua berperan penting dalam menyelesaikan persamaan kuadrat dan sistem persamaan. Persamaan kuadrat dapat diselesaikan menggunakan rumus kuadrat, yang melibatkan operasi akar pangkat dua.
-
Geometri
Akar pangkat dua digunakan dalam menghitung panjang sisi miring segitiga siku-siku menggunakan Teorema Pythagoras. Selain itu, akar pangkat dua digunakan dalam menghitung luas dan volume bangun ruang, seperti kubus dan bola.
-
Trigonometri
Akar pangkat dua muncul dalam fungsi trigonometri seperti sinus dan kosinus. Fungsi-fungsi ini digunakan untuk menghitung sisi dan sudut segitiga, serta menyelesaikan masalah yang melibatkan gerakan periodik.
-
Kalkulus
Akar pangkat dua digunakan dalam konsep turunan dan integral. Turunan dari fungsi kuadrat melibatkan operasi akar pangkat dua, dan integral dari beberapa fungsi dapat dihitung menggunakan substitusi akar pangkat dua.
Kaitan akar pangkat dua dengan topik-topik ini menyoroti sifat serbagunanya dan pentingnya dalam berbagai bidang matematika. Memahami hubungan ini sangat penting untuk menguasai konsep matematika yang lebih kompleks dan menerapkannya dalam memecahkan masalah di dunia nyata.
Berikut adalah beberapa pertanyaan umum tentang akar pangkat 2 yang mungkin Anda miliki:
Pertanyaan 1: Apa definisi akar pangkat 2?
Akar pangkat 2 dari suatu bilangan adalah bilangan yang, jika dikuadratkan, akan menghasilkan bilangan asli tersebut. Misalnya, akar pangkat 2 dari 9 adalah 3 karena 3 x 3 = 9.
Pertanyaan 2: Bagaimana cara menghitung akar pangkat 2?
Ada beberapa cara untuk menghitung akar pangkat 2. Salah satu cara yang umum adalah dengan menggunakan kalkulator. Cara lainnya adalah dengan menggunakan tabel akar pangkat 2 atau dengan melakukan perkiraan menggunakan metode iteratif.
Pertanyaan 3: Apa saja aplikasi akar pangkat 2?
Akar pangkat 2 memiliki banyak aplikasi dalam berbagai bidang, termasuk matematika, fisika, dan teknik. Beberapa contoh penerapan akar pangkat 2 antara lain menyelesaikan persamaan kuadrat, menghitung jarak dan luas, serta memahami konsep-konsep fisika seperti percepatan dan energi.
Pertanyaan 4: Apa saja sifat-sifat akar pangkat 2?
Akar pangkat 2 memiliki beberapa sifat yang berguna, seperti sifat distributif, asosiatif, identitas, dan invers. Sifat-sifat ini dapat digunakan untuk menyederhanakan operasi yang melibatkan akar pangkat 2 dan menyelesaikan masalah matematika dengan lebih mudah.
Dengan memahami definisi, cara menghitung, aplikasi, dan sifat-sifat akar pangkat 2, Anda dapat menggunakan konsep penting ini secara efektif untuk memecahkan masalah dan memahami konsep matematika dan fisika yang lebih kompleks.
Tips: Untuk mempelajari lebih lanjut tentang akar pangkat 2, Anda dapat membaca buku teks matematika, menjelajahi sumber daya online, atau berkonsultasi dengan guru atau tutor. Dengan latihan dan pemahaman yang baik, Anda dapat menguasai konsep akar pangkat 2 dan menerapkannya dalam berbagai situasi.
Tips Menguasai Akar Pangkat Dua
Untuk menguasai konsep akar pangkat dua, beberapa tips berikut dapat membantu:
Tip 1: Pahami Definisi dan Sifat
Memahami definisi akar pangkat dua sebagai bilangan yang jika dikuadratkan menghasilkan bilangan asli, serta sifat-sifatnya seperti sifat distributif dan asosiatif, sangat penting. Pemahaman ini menjadi dasar untuk operasi dan aplikasi akar pangkat dua.
Tip 2: Berlatih Menghitung
Latihan yang konsisten dalam menghitung akar pangkat dua menggunakan berbagai metode, seperti kalkulator, tabel, atau estimasi iteratif, akan meningkatkan keterampilan dan kecepatan Anda.
Tip 3: Terapkan dalam Konteks
Terapkan operasi akar pangkat dua dalam konteks soal matematika dan fisika untuk memahami aplikasinya dalam menyelesaikan persamaan kuadrat, menghitung jarak, dan memahami konsep fisika seperti percepatan dan energi.
Tip 4: Manfaatkan Sumber Belajar
Gunakan buku teks, sumber online, atau konsultasikan dengan guru/tutor untuk memperjelas konsep dan memperluas pengetahuan Anda tentang akar pangkat dua.
Dengan mengikuti tips ini dan berlatih secara teratur, Anda dapat meningkatkan pemahaman dan keterampilan Anda dalam menangani akar pangkat dua, sehingga memperluas kemampuan matematika dan fisika Anda.
Kesimpulan
Konsep akar pangkat dua berperan krusial dalam berbagai bidang, mulai dari matematika hingga fisika dan teknik. Pemahaman yang kuat tentang definisi, sifat, dan aplikasinya sangat penting untuk menyelesaikan masalah matematika, memahami konsep fisika, dan menguasai topik-topik matematika tingkat lanjut.
Dengan berlatih secara konsisten, memanfaatkan sumber belajar, dan menerapkan pemahaman kita dalam konteks nyata, kita dapat menguasai konsep akar pangkat dua dan memanfaatkan kekuatannya untuk mengeksplorasi konsep matematika dan fisika yang lebih kompleks. Akar pangkat dua akan terus menjadi alat yang sangat diperlukan dalam perjalanan kita untuk memahami dunia kuantitatif di sekitar kita.
