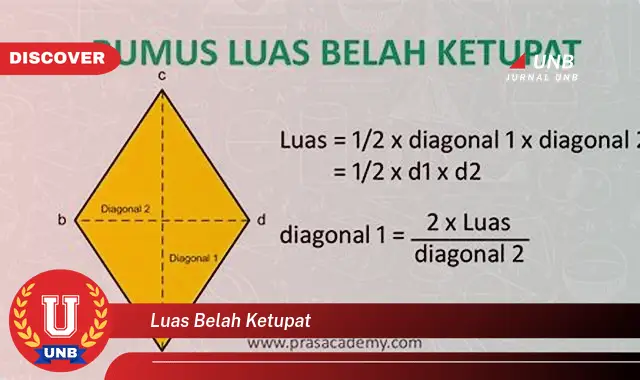
Luas belah ketupat adalah besaran yang menyatakan ukuran daerah yang ditempati oleh sebuah belah ketupat. Belah ketupat merupakan bangun datar dua dimensi yang memiliki empat sisi sama panjang dan dua pasang sudut yang berhadapan sama besar. Untuk menghitung luas belah ketupat, digunakan rumus: Luas = (Diagonal 1 x Diagonal 2) / 2.
Mengetahui luas belah ketupat sangat penting dalam berbagai bidang, seperti arsitektur, desain interior, dan teknik sipil. Dengan mengetahui luas belah ketupat, kita dapat menentukan kebutuhan material, merencanakan tata letak, dan menghitung biaya konstruksi secara akurat. Selain itu, konsep luas belah ketupat juga memiliki sejarah panjang dalam matematika, yang dapat ditelusuri kembali ke zaman dahulu.
Pada artikel ini, kita akan membahas lebih dalam tentang luas belah ketupat, termasuk rumus untuk menghitungnya, sifat-sifatnya, dan penerapannya dalam kehidupan sehari-hari. Kita juga akan mengeksplorasi sejarah dan perkembangan konsep luas belah ketupat dalam matematika.
Luas Belah Ketupat
Luas belah ketupat merupakan besaran yang sangat penting dalam berbagai bidang, seperti arsitektur, desain interior, dan teknik sipil. Berikut adalah tujuh aspek penting yang terkait dengan luas belah ketupat:
- Rumus: Luas belah ketupat = (Diagonal 1 x Diagonal 2) / 2
- Satuan: Luas belah ketupat dinyatakan dalam satuan luas, seperti meter persegi (m) atau sentimeter persegi (cm)
- Sifat: Luas belah ketupat tidak berubah jika belah ketupat diputar atau dibalik
- Penerapan: Luas belah ketupat digunakan untuk menentukan kebutuhan material, merencanakan tata letak, dan menghitung biaya konstruksi
- Sejarah: Konsep luas belah ketupat telah dikenal sejak zaman dahulu, dan telah digunakan dalam berbagai aplikasi praktis
- Matematika: Luas belah ketupat terkait dengan konsep geometri dan trigonometri
- Contoh: Sebuah belah ketupat dengan diagonal 10 cm dan 15 cm memiliki luas 75 cm
Ketujuh aspek ini saling terkait dan memberikan pemahaman yang komprehensif tentang luas belah ketupat. Misalnya, rumus luas belah ketupat digunakan dalam penerapan praktis untuk menghitung kebutuhan material dan biaya konstruksi. Selain itu, konsep luas belah ketupat dalam matematika terkait dengan sifat-sifat geometri dan trigonometri, yang digunakan dalam berbagai aplikasi, seperti arsitektur dan desain.
Rumus
Rumus ini merupakan dasar untuk menghitung luas belah ketupat. Diagonal 1 dan Diagonal 2 adalah dua garis yang menghubungkan titik-titik sudut belah ketupat yang berlawanan. Dengan menggunakan rumus ini, kita dapat menentukan luas belah ketupat tanpa harus mengetahui panjang sisinya.
Memahami rumus ini sangat penting karena memungkinkan kita untuk menghitung luas belah ketupat dalam berbagai situasi praktis. Misalnya, dalam arsitektur, rumus ini digunakan untuk menentukan kebutuhan material untuk membangun struktur yang melibatkan belah ketupat, seperti atap atau dinding. Dalam desain interior, rumus ini digunakan untuk merencanakan tata letak ruangan yang melibatkan belah ketupat, seperti lantai atau langit-langit. Dalam teknik sipil, rumus ini digunakan untuk menghitung beban yang dapat ditopang oleh struktur yang melibatkan belah ketupat, seperti jembatan atau gedung.
Selain aplikasi praktisnya, rumus luas belah ketupat juga memiliki signifikansi matematis. Rumus ini terkait dengan konsep geometri dan trigonometri, dan dapat digunakan untuk membuktikan sifat-sifat belah ketupat lainnya. Misalnya, rumus ini dapat digunakan untuk membuktikan bahwa diagonal-diagonal belah ketupat saling tegak lurus.
Satuan
Luas belah ketupat merupakan besaran yang menyatakan ukuran daerah yang ditempati oleh sebuah belah ketupat. Untuk menyatakan besaran luas belah ketupat, diperlukan satuan luas yang sesuai, seperti meter persegi (m) atau sentimeter persegi (cm).
-
Satuan Internasional (SI)
Dalam Sistem Internasional (SI), satuan luas yang digunakan adalah meter persegi (m). Satuan ini digunakan secara luas dalam berbagai bidang, seperti arsitektur, teknik sipil, dan desain interior. Misalnya, luas sebuah ruangan dihitung dalam meter persegi untuk menentukan kebutuhan material lantai atau cat.
-
Satuan Non-SI
Selain meter persegi, terdapat beberapa satuan luas non-SI yang masih digunakan dalam kehidupan sehari-hari, seperti sentimeter persegi (cm). Satuan ini sering digunakan untuk menyatakan luas benda-benda kecil, seperti kertas atau kain. Misalnya, luas sebuah kartu pos dihitung dalam sentimeter persegi untuk menentukan biaya perangko.
-
Pentingnya Satuan yang Tepat
Menggunakan satuan luas yang tepat sangat penting untuk memastikan akurasi dan konsistensi dalam pengukuran luas belah ketupat. Misalnya, jika luas sebuah ruangan dihitung dalam sentimeter persegi, maka kebutuhan material lantai juga harus dihitung dalam sentimeter persegi agar sesuai. Hal ini akandan kesalahan dalam perencanaan dan pelaksanaan.
-
Konversi Satuan
Terkadang, diperlukan untuk mengonversi luas belah ketupat dari satu satuan ke satuan lainnya. Misalnya, jika luas sebuah ruangan diketahui dalam sentimeter persegi, tetapi kebutuhan material lantai dinyatakan dalam meter persegi, maka luas ruangan harus dikonversi ke meter persegi terlebih dahulu. Rumus konversi yang digunakan adalah: 1 m = 10.000 cm.
Dengan memahami satuan luas yang tepat dan cara mengonversinya, kita dapat memastikan bahwa luas belah ketupat diukur dan dinyatakan dengan benar, sehingga mendukung pengambilan keputusan dan perencanaan yang akurat dalam berbagai bidang.
Sifat
Sifat ini merupakan salah satu sifat penting belah ketupat yang membedakannya dari bangun datar lainnya. Sifat ini menyatakan bahwa luas belah ketupat tetap sama, berapa pun kali belah ketupat tersebut diputar atau dibalik.
-
Konsistensi Luas
Sifat ini menjamin bahwa luas belah ketupat tetap konsisten, tidak peduli bagaimana belah ketupat tersebut diorientasikan. Hal ini sangat penting dalam aplikasi praktis, seperti arsitektur dan desain interior, di mana luas belah ketupat digunakan untuk menentukan kebutuhan material dan merencanakan tata letak.
-
Implikasi Geometris
Sifat ini memiliki implikasi geometris yang mendalam. Ini menunjukkan bahwa simetri belah ketupat, baik rotasi maupun refleksi, tidak memengaruhi luasnya. Hal ini terkait dengan konsep invariansi, yang banyak ditemukan dalam matematika dan fisika.
-
Contoh Nyata
Dalam kehidupan nyata, sifat ini dapat diamati pada berbagai objek, seperti lantai keramik berbentuk belah ketupat atau atap rumah yang menggunakan genteng belah ketupat. Luas lantai atau atap tetap sama, meskipun objek-objek tersebut diputar atau dibalik selama proses pemasangan.
-
Penerapan dalam Matematika
Sifat ini juga memiliki aplikasi penting dalam matematika. Ini digunakan dalam pembuktian teorema geometri, seperti teorema Pythagoras dan teorema luas jajaran genjang. Selain itu, sifat ini digunakan dalam kalkulus integral untuk menghitung luas daerah yang dibatasi oleh kurva belah ketupat.
Dengan memahami sifat ini, kita dapat memperoleh wawasan yang lebih dalam tentang geometri belah ketupat dan menerapkannya secara efektif dalam berbagai bidang, baik praktis maupun teoritis.
Penerapan
Luas belah ketupat memiliki peran penting dalam berbagai bidang praktis, terutama dalam arsitektur, desain interior, dan teknik sipil. Berikut adalah beberapa penerapan pentingnya:
-
Penentuan Kebutuhan Material
Luas belah ketupat digunakan untuk menentukan jumlah material yang dibutuhkan untuk membangun atau merenovasi struktur yang melibatkan belah ketupat. Misalnya, dalam arsitektur, luas atap belah ketupat digunakan untuk menghitung kebutuhan genteng atau bahan atap lainnya.
-
Perencanaan Tata Letak
Luas belah ketupat juga digunakan untuk merencanakan tata letak ruang yang melibatkan belah ketupat. Misalnya, dalam desain interior, luas lantai belah ketupat digunakan untuk menentukan penempatan furnitur dan perlengkapan lainnya secara efisien.
-
Penghitungan Biaya Konstruksi
Selain itu, luas belah ketupat digunakan untuk menghitung biaya konstruksi. Dengan mengetahui luas belah ketupat, kontraktor dapat memperkirakan biaya material, tenaga kerja, dan faktor lainnya yang terlibat dalam pembangunan.
Penerapan luas belah ketupat ini sangat penting untuk memastikan bahwa struktur atau ruang yang dibangun sesuai dengan kebutuhan dan anggaran yang telah ditentukan. Dengan memahami penerapan luas belah ketupat, para profesional di berbagai bidang dapat membuat keputusan yang tepat dan mengoptimalkan penggunaan sumber daya.
Sejarah
Konsep luas belah ketupat telah dikenal sejak zaman dahulu dan telah digunakan dalam berbagai aplikasi praktis. Pemahaman tentang luas belah ketupat sangat penting karena memungkinkan perhitungan akurat kebutuhan material, perencanaan tata letak yang efisien, dan estimasi biaya konstruksi yang tepat.
-
Penggunaan dalam Arsitektur Kuno
Konsep luas belah ketupat telah digunakan dalam arsitektur sejak zaman kuno. Bangsa Mesir kuno menggunakan belah ketupat dalam desain piramida mereka, dan bangsa Romawi menggunakannya dalam pembangunan jalan dan akuaduk. -
Aplikasi dalam Seni dan Kerajinan
Luas belah ketupat juga telah digunakan dalam seni dan kerajinan selama berabad-abad. Seniman dan pengrajin telah menggunakan belah ketupat untuk membuat pola dekoratif pada tekstil, keramik, dan perhiasan. -
Penggunaan dalam Pertanian
Dalam bidang pertanian, luas belah ketupat digunakan untuk menentukan luas lahan pertanian dan memperkirakan hasil panen. Hal ini penting untuk perencanaan produksi dan pemasaran. -
Relevansi dalam Matematika Modern
Konsep luas belah ketupat masih relevan dalam matematika modern. Ini digunakan dalam geometri untuk menghitung luas bangun datar lainnya, seperti jajaran genjang dan trapesium. Selain itu, luas belah ketupat memiliki aplikasi dalam kalkulus dan fisika.
Dengan memahami sejarah dan aplikasi praktis luas belah ketupat, kita dapat memperoleh apresiasi yang lebih dalam tentang pentingnya konsep ini dalam berbagai bidang. Ini tidak hanya membantu kita memahami pencapaian masa lalu tetapi juga menginformasikan praktik kita saat ini dan masa depan.
Matematika
Konsep luas belah ketupat memiliki hubungan yang kuat dengan konsep geometri dan trigonometri. Dalam geometri, luas belah ketupat digunakan untuk menghitung luas bangun datar lainnya, seperti jajaran genjang dan trapesium. Sementara itu, dalam trigonometri, luas belah ketupat digunakan untuk menghitung luas segitiga dan menentukan nilai fungsi trigonometri.
-
Menghitung Luas Bangun Datar Lainnya
Luas belah ketupat berperan penting dalam menghitung luas bangun datar lainnya yang memiliki bentuk serupa, seperti jajaran genjang dan trapesium. Dengan mengetahui luas belah ketupat dan menerapkan rumus tertentu, kita dapat menentukan luas bangun datar tersebut dengan mudah. -
Menghitung Luas Segitiga
Luas belah ketupat juga terkait dengan luas segitiga. Jika sebuah segitiga dibagi menjadi dua bagian sama besar oleh sebuah garis tinggi, maka masing-masing bagian tersebut akan membentuk sebuah belah ketupat. Dengan mengetahui luas belah ketupat tersebut, kita dapat menentukan luas segitiga dengan mudah. -
Menentukan Nilai Fungsi Trigonometri
Dalam trigonometri, luas belah ketupat digunakan untuk menentukan nilai fungsi trigonometri, seperti sinus dan kosinus. Dengan mengetahui luas belah ketupat dan panjang diagonalnya, kita dapat menghitung nilai fungsi trigonometri tersebut menggunakan rumus tertentu. -
Aplikasi Praktis
Hubungan antara luas belah ketupat dengan geometri dan trigonometri memiliki banyak aplikasi praktis dalam berbagai bidang, seperti arsitektur, teknik sipil, dan desain interior. Misalnya, dalam arsitektur, konsep ini digunakan untuk menghitung luas atap dan dinding bangunan, sedangkan dalam teknik sipil digunakan untuk menentukan luas jembatan dan jalan.
Dengan memahami hubungan antara luas belah ketupat dengan geometri dan trigonometri, kita dapat memperoleh pemahaman yang lebih komprehensif tentang konsep luas belah ketupat dan penerapannya dalam berbagai bidang.
Contoh
Contoh ini mengilustrasikan penerapan rumus luas belah ketupat dalam kehidupan nyata. Dengan mengetahui panjang diagonal belah ketupat, kita dapat menghitung luasnya menggunakan rumus: Luas = (Diagonal 1 x Diagonal 2) / 2.
Dalam contoh ini, diagonal 1 berukuran 10 cm dan diagonal 2 berukuran 15 cm. Dengan mensubstitusikan nilai-nilai ini ke dalam rumus, kita memperoleh: Luas = (10 cm x 15 cm) / 2 = 75 cm.
Pemahaman tentang cara menghitung luas belah ketupat sangat penting dalam berbagai bidang, seperti arsitektur, desain interior, dan teknik sipil. Dengan mengetahui luas belah ketupat, para profesional di bidang ini dapat menentukan kebutuhan material, merencanakan tata letak ruang, dan menghitung biaya konstruksi secara akurat.
Contoh ini menunjukkan pentingnya memahami konsep luas belah ketupat dan penerapannya dalam kehidupan nyata. Dengan memahami konsep ini, kita dapat membuat keputusan yang tepat dan mengoptimalkan penggunaan sumber daya dalam berbagai proyek.
Pertanyaan Umum tentang Luas Belah Ketupat
Bagian ini akan membahas pertanyaan umum yang sering diajukan mengenai luas belah ketupat. Dengan memahami jawaban atas pertanyaan-pertanyaan ini, kita dapat memperoleh pemahaman yang lebih komprehensif tentang konsep luas belah ketupat dan penerapannya.
Pertanyaan 1: Apa saja rumus untuk menghitung luas belah ketupat?
Rumus untuk menghitung luas belah ketupat adalah:
- Luas = (Diagonal 1 x Diagonal 2) / 2
Pertanyaan 2: Satuan apakah yang digunakan untuk menyatakan luas belah ketupat?
Luas belah ketupat dinyatakan dalam satuan luas, seperti meter persegi (m2), sentimeter persegi (cm2), atau milimeter persegi (mm2).
Pertanyaan 3: Mengapa penting untuk mengetahui luas belah ketupat?
Mengetahui luas belah ketupat penting untuk berbagai aplikasi praktis, seperti menentukan kebutuhan material, merencanakan tata letak ruang, dan menghitung biaya konstruksi. Pemahaman tentang luas belah ketupat memungkinkan pengambilan keputusan yang tepat dan pengoptimalan penggunaan sumber daya.
Pertanyaan 4: Dalam bidang apa saja konsep luas belah ketupat digunakan?
Konsep luas belah ketupat digunakan dalam berbagai bidang, termasuk arsitektur, desain interior, teknik sipil, matematika, dan seni. Pemahaman tentang luas belah ketupat sangat penting untuk perhitungan akurat, perencanaan yang efisien, dan penciptaan desain yang estetis.
Dengan memahami pertanyaan dan jawaban umum ini, kita dapat memperoleh wawasan yang lebih mendalam tentang luas belah ketupat dan penerapannya yang luas.
Tips untuk Menghitung Luas Belah Ketupat:
Tips Menghitung Luas Belah Ketupat
Untuk memastikan akurasi dan efisiensi dalam menghitung luas belah ketupat, berikut beberapa tips yang perlu diperhatikan:
Tip 1: Pastikan Diagonal Diketahui
Rumus luas belah ketupat memerlukan panjang kedua diagonal. Pastikan Anda memiliki informasi yang benar dan akurat mengenai panjang diagonal tersebut.
Tip 2: Gunakan Rumus dengan Benar
Rumus luas belah ketupat adalah (Diagonal 1 x Diagonal 2) / 2. Pastikan Anda menerapkan rumus ini dengan benar dan menggunakan satuan yang sesuai.
Tip 3: Periksa Satuan
Luas belah ketupat dinyatakan dalam satuan luas, seperti meter persegi (m2) atau sentimeter persegi (cm2). Periksa satuan yang digunakan dalam soal dan pastikan Anda menggunakan satuan yang sama saat menghitung luas.
Tip 4: Gambar Belah Ketupat
Jika memungkinkan, gambarlah belah ketupat yang akan dihitung luasnya. Hal ini dapat membantu Anda memvisualisasikan bentuk dan mengidentifikasi diagonal-diagonalnya dengan lebih jelas.
Dengan mengikuti tips ini, Anda dapat meningkatkan akurasi dan efisiensi dalam menghitung luas belah ketupat, sehingga mendukung pengambilan keputusan dan perencanaan yang tepat dalam berbagai bidang.
Kesimpulan
Luas belah ketupat merupakan konsep fundamental dalam geometri yang memiliki berbagai aplikasi praktis di berbagai bidang, seperti arsitektur, desain interior, dan teknik sipil. Dengan memahami rumus, sifat, dan penerapan luas belah ketupat, kita dapat melakukan perhitungan akurat, merencanakan tata letak secara efisien, dan mengoptimalkan penggunaan sumber daya.
Konsep luas belah ketupat terus berkembang dan diterapkan dalam konteks baru. Pemahaman yang komprehensif tentang topik ini sangat penting bagi para profesional, peneliti, dan siapa pun yang ingin memahami prinsip-prinsip dasar geometri dan penerapannya di dunia nyata. Dengan terus mengeksplorasi dan menguasai konsep luas belah ketupat, kita memperkaya pengetahuan kita dan berkontribusi pada kemajuan di berbagai bidang.









