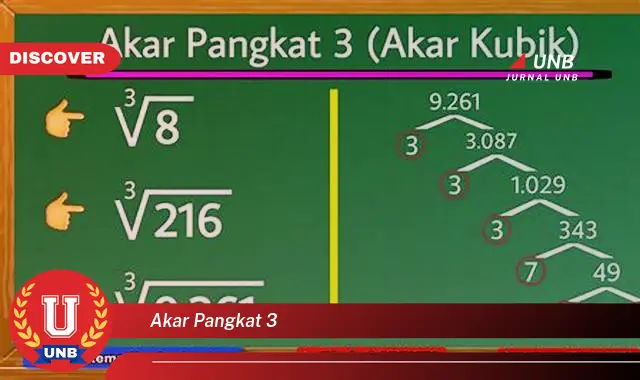
Pengertian dan Contoh Akar Pangkat 3
Akar pangkat 3 atau kubik adalah operasi matematika yang mencari nilai yang jika dipangkatkan tiga akan menghasilkan bilangan tertentu. Misalnya, akar pangkat 3 dari 27 adalah 3, karena 3 pangkat 3 sama dengan 27.
Manfaat dan Pentingnya Akar Pangkat 3
Akar pangkat 3 memiliki banyak aplikasi penting dalam berbagai bidang, seperti:
- Fisika: Menghitung gaya, kecepatan, dan percepatan.
- Kimia: Menentukan konsentrasi zat dalam larutan.
- Matematika: Memecahkan persamaan kubik.
- Statistika: Menghitung nilai rata-rata dan standar deviasi.
Sejarah dan Perkembangan Akar Pangkat 3
Konsep akar pangkat 3 telah dikenal sejak zaman kuno. Bangsa Babilonia dan Mesir Kuno menggunakannya untuk menghitung volume dan menyelesaikan masalah matematika. Pada abad ke-16, matematikawan Italia Niccol Tartaglia mempopulerkan metode untuk menghitung akar pangkat 3.
Topik Utama Artikel
Artikel ini akan membahas topik-topik berikut terkait akar pangkat 3:
- Cara menghitung akar pangkat 3 secara manual dan menggunakan kalkulator.
- Sifat-sifat akar pangkat 3.
- Aplikasi akar pangkat 3 dalam berbagai bidang.
- Sejarah dan perkembangan akar pangkat 3.
akar pangkat 3
Akar pangkat 3 merupakan konsep matematika yang penting dengan beragam aspek. Berikut adalah tujuh aspek utama yang perlu diperhatikan:
- Definisi: Mencari nilai yang dipangkatkan tiga menghasilkan bilangan tertentu.
- Notasi: Menggunakan simbol .
- Sifat: Memenuhi sifat-sifat dasar operasi pangkat.
- Aplikasi: Digunakan dalam berbagai bidang seperti fisika, kimia, dan matematika.
- Metode Hitung: Dapat dihitung manual atau menggunakan kalkulator.
- Sejarah: Dikenal sejak zaman kuno oleh bangsa Babilonia dan Mesir.
- Contoh: 8 = 2 karena 2 pangkat 3 = 8.
Aspek-aspek tersebut saling terkait dan membentuk dasar pemahaman tentang akar pangkat 3. Definisi dan notasi memberikan landasan konseptual, sedangkan sifat dan aplikasi menunjukkan pentingnya dan kegunaannya. Metode hitung dan sejarah memberikan wawasan praktis dan kontekstual, sementara contoh memperjelas konsep secara konkret. Dengan memahami aspek-aspek ini, individu dapat memperoleh pemahaman yang komprehensif tentang akar pangkat 3 dan penerapannya dalam berbagai bidang.
Definisi: Mencari nilai yang dipangkatkan tiga menghasilkan bilangan tertentu.
Definisi akar pangkat 3 merupakan landasan konseptual yang mendasari operasi matematika ini. Definisi tersebut menjelaskan bahwa akar pangkat 3 dari suatu bilangan adalah nilai yang, jika dipangkatkan tiga, akan menghasilkan bilangan tersebut. Dengan kata lain, akar pangkat 3 adalah kebalikan dari operasi pangkat tiga.
Definisi ini sangat penting karena memberikan pemahaman yang jelas tentang apa itu akar pangkat 3 dan bagaimana cara kerjanya. Tanpa definisi ini, akan sulit untuk memahami dan menggunakan operasi akar pangkat 3 secara efektif.
Sebagai contoh, akar pangkat 3 dari 8 adalah 2, karena 2 pangkat 3 sama dengan 8. Definisi ini membantu kita memahami bahwa akar pangkat 3 dari suatu bilangan adalah nilai yang, jika dipangkatkan tiga, akan menghasilkan bilangan asli tersebut.
Memahami definisi akar pangkat 3 sangat penting untuk dapat menggunakan operasi ini dengan benar. Definisi ini menjadi dasar bagi sifat-sifat, metode perhitungan, dan aplikasi akar pangkat 3 dalam berbagai bidang.
Notasi: Menggunakan Simbol
Notasi akar pangkat tiga menggunakan simbol khusus , yang ditempatkan di depan bilangan yang akan dicari akar pangkat tiganya. Simbol ini menunjukkan bahwa operasi akar pangkat tiga akan dilakukan pada bilangan tersebut.
-
Penulisan Simbol
Penulisan simbol harus tepat agar operasi akar pangkat tiga dapat dibedakan dengan jelas dari operasi matematika lainnya. Simbol ini ditulis dengan ukuran yang lebih kecil dan agak di atas bilangan yang akan dicari akar pangkat tiganya, seperti pada contoh berikut: 8
-
Penggunaan dalam Persamaan
Dalam persamaan matematika, simbol digunakan untuk menyatakan operasi akar pangkat tiga pada suatu variabel atau konstanta. Misalnya, dalam persamaan x = 2, simbol menunjukkan bahwa akar pangkat tiga dari variabel x adalah 2.
-
Konsistensi Penulisan
Penting untuk menggunakan notasi akar pangkat tiga secara konsisten dalam operasi matematika. Hal ini untuk menghindari kebingungan dan memastikan bahwa operasi tersebut dilakukan dengan benar. Penulisan yang konsisten juga memudahkan pembacaan dan pemahaman persamaan matematika.
-
Penggunaan Kalkulator
Kalkulator ilmiah biasanya memiliki tombol khusus untuk menghitung akar pangkat tiga. Tombol ini biasanya diberi label “” atau “x^(1/3)”. Untuk menggunakannya, cukup masukkan bilangan yang ingin dicari akar pangkat tiganya dan tekan tombol tersebut.
Dengan memahami notasi akar pangkat tiga dengan benar, individu dapat melakukan operasi matematika yang melibatkan akar pangkat tiga dengan lebih mudah dan akurat.
Sifat: Memenuhi Sifat-sifat Dasar Operasi Pangkat
Akar pangkat tiga memiliki sifat-sifat dasar yang sama seperti operasi pangkat lainnya. Sifat-sifat ini sangat penting untuk memahami dan menggunakan akar pangkat tiga dengan benar.
Salah satu sifat penting akar pangkat tiga adalah sifat asosiatif, yaitu akar pangkat tiga dari suatu bilangan yang dipangkatkan tiga sama dengan bilangan itu sendiri. Misalnya, .
Sifat penting lainnya adalah sifat distributif, yaitu akar pangkat tiga dari hasil kali dua bilangan sama dengan hasil kali akar pangkat tiga masing-masing bilangan. Misalnya, .
Memahami sifat-sifat akar pangkat tiga sangat penting untuk dapat menyelesaikan berbagai masalah matematika. Misalnya, sifat asosiatif dapat digunakan untuk menyederhanakan persamaan, dan sifat distributif dapat digunakan untuk mengalikan atau membagi bilangan yang mengandung akar pangkat tiga.
Selain itu, sifat-sifat akar pangkat tiga juga memiliki aplikasi dalam berbagai bidang, seperti fisika dan kimia. Misalnya, dalam fisika, sifat asosiatif digunakan untuk menghitung kecepatan benda yang bergerak dengan percepatan konstan.
Dengan memahami sifat-sifat akar pangkat tiga, individu dapat menggunakan operasi ini dengan lebih efektif dan efisien dalam berbagai aplikasi matematika dan bidang lainnya.
Aplikasi: Digunakan dalam Berbagai Bidang Seperti Fisika, Kimia, dan Matematika
Akar pangkat tiga memiliki aplikasi yang luas dalam berbagai bidang, termasuk fisika, kimia, dan matematika. Aplikasi-aplikasi ini menunjukkan pentingnya akar pangkat tiga sebagai konsep matematika yang fundamental.
Dalam fisika, akar pangkat tiga digunakan untuk menghitung volume benda beraturan, seperti kubus dan bola. Misalnya, untuk menghitung volume kubus, digunakan rumus V = s, di mana s adalah panjang rusuk kubus. Akar pangkat tiga juga digunakan dalam persamaan gerak, seperti persamaan untuk menghitung kecepatan benda yang bergerak dengan percepatan konstan.
Dalam kimia, akar pangkat tiga digunakan untuk menghitung konsentrasi zat dalam larutan. Misalnya, untuk menghitung konsentrasi molar suatu larutan, digunakan rumus M = n/V, di mana M adalah konsentrasi molar, n adalah jumlah mol zat terlarut, dan V adalah volume larutan dalam liter. Akar pangkat tiga juga digunakan dalam persamaan kesetimbangan kimia, seperti persamaan untuk menghitung tetapan kesetimbangan.
Dalam matematika, akar pangkat tiga digunakan untuk menyelesaikan persamaan kubik, yaitu persamaan polinomial yang memiliki pangkat tertinggi tiga. Akar pangkat tiga juga digunakan dalam teori bilangan, seperti untuk menentukan apakah suatu bilangan adalah bilangan prima atau komposit.
Memahami aplikasi akar pangkat tiga dalam berbagai bidang sangatlah penting. Hal ini memungkinkan individu untuk menggunakan akar pangkat tiga secara efektif dalam memecahkan masalah di berbagai bidang studi dan aplikasi praktis.
Metode Hitung: Dapat dihitung manual atau menggunakan kalkulator
Akar pangkat tiga dapat dihitung menggunakan berbagai metode, baik secara manual maupun dengan bantuan kalkulator. Masing-masing metode memiliki kelebihan dan kekurangannya sendiri, tergantung pada tingkat kesulitan perhitungan dan ketersediaan alat bantu.
-
Metode Manual
Metode manual untuk menghitung akar pangkat tiga melibatkan penggunaan algoritma tertentu, seperti metode bagi tiga atau metode Newton-Raphson. Metode ini membutuhkan ketelitian dan ketekunan, terutama untuk bilangan yang besar atau perhitungan yang kompleks.
-
Metode Kalkulator
Kalkulator ilmiah biasanya memiliki fungsi khusus untuk menghitung akar pangkat tiga. Metode ini sangat mudah dan cepat, memberikan hasil yang akurat hingga beberapa digit desimal. Kalkulator juga dapat digunakan untuk menghitung akar pangkat tiga dari bilangan yang sangat besar atau bilangan dengan banyak digit desimal.
Pemilihan metode hitung akar pangkat tiga bergantung pada kebutuhan dan situasi spesifik. Untuk perhitungan sederhana atau perkiraan, metode manual dapat digunakan. Namun, untuk perhitungan yang lebih kompleks atau membutuhkan hasil yang sangat akurat, metode kalkulator lebih disarankan.
Sejarah: Dikenal sejak zaman kuno oleh bangsa Babilonia dan Mesir.
Konsep akar pangkat tiga telah dikenal sejak zaman kuno, dengan bukti penggunaannya ditemukan dalam peradaban Babilonia dan Mesir. Pemahaman awal mereka tentang akar pangkat tiga memainkan peran penting dalam perkembangan matematika dan aplikasinya dalam berbagai bidang.
Bangsa Babilonia menggunakan akar pangkat tiga dalam sistem metrologi mereka, yang melibatkan penggunaan sistem bilangan seksagesimal (basis 60). Mereka mengembangkan metode untuk menghitung akar pangkat tiga menggunakan algoritma perkiraan, yang menunjukkan pemahaman mereka tentang konsep ini.
Sementara itu, bangsa Mesir menggunakan akar pangkat tiga dalam arsitektur dan konstruksi. Mereka menggunakannya untuk menentukan volume piramida dan struktur lainnya, yang menunjukkan pentingnya konsep ini dalam aplikasi praktis.
Pemahaman tentang akar pangkat tiga yang dikembangkan oleh peradaban kuno ini menjadi dasar bagi pengembangan lebih lanjut konsep ini oleh matematikawan di kemudian hari. Hal ini berkontribusi pada pemahaman yang lebih mendalam tentang matematika dan aplikasinya yang luas dalam berbagai disiplin ilmu.
Contoh: 38 = 2 karena 2 pangkat 3 = 8.
Contoh ini menunjukkan hubungan antara akar pangkat tiga dan operasi pangkat. Akar pangkat tiga dari 8 adalah 2, karena jika 2 dipangkatkan tiga, hasilnya adalah 8. Contoh ini membantu memahami konsep akar pangkat tiga sebagai kebalikan dari operasi pangkat tiga.
-
Fungsi Akar Pangkat Tiga
Akar pangkat tiga digunakan untuk mencari nilai yang, jika dipangkatkan tiga, menghasilkan bilangan tertentu. Dalam contoh ini, akar pangkat tiga dari 8 adalah 2, karena 2 = 8.
-
Notasi Akar Pangkat Tiga
Simbol 3 digunakan untuk menunjukkan operasi akar pangkat tiga. Dalam contoh ini, 38 dibaca sebagai “akar pangkat tiga dari 8”.
-
Sifat Akar Pangkat Tiga
Akar pangkat tiga memiliki sifat-sifat tertentu, salah satunya adalah sifat kebalikan dari operasi pangkat tiga. Contoh ini menunjukkan sifat tersebut, yaitu 3(2) = 2.
-
Aplikasi Akar Pangkat Tiga
Akar pangkat tiga memiliki banyak aplikasi dalam matematika dan bidang lainnya. Misalnya, dalam fisika, akar pangkat tiga digunakan untuk menghitung volume benda beraturan, seperti kubus dan bola.
Dengan memahami hubungan antara contoh ini dan konsep akar pangkat tiga, individu dapat memperoleh pemahaman yang lebih mendalam tentang operasi matematika penting ini dan aplikasinya yang luas.
Pertanyaan Umum tentang Akar Pangkat Tiga
Bagian ini membahas beberapa pertanyaan umum seputar konsep akar pangkat tiga, memberikan pemahaman yang lebih mendalam tentang topik ini.
Pertanyaan 1: Apa itu akar pangkat tiga?
Akar pangkat tiga adalah operasi matematika yang mencari nilai yang, jika dipangkatkan tiga, akan menghasilkan bilangan tertentu. Misalnya, akar pangkat tiga dari 8 adalah 2, karena 2 pangkat 3 sama dengan 8.
Pertanyaan 2: Bagaimana cara menghitung akar pangkat tiga?
Akar pangkat tiga dapat dihitung secara manual atau menggunakan kalkulator. Metode manual melibatkan penggunaan algoritma atau rumus tertentu, sedangkan metode kalkulator memberikan hasil yang lebih cepat dan akurat.
Pertanyaan 3: Apa saja sifat-sifat akar pangkat tiga?
Akar pangkat tiga memiliki beberapa sifat dasar, seperti sifat asosiatif dan distributif. Sifat-sifat ini memudahkan penyederhanaan dan penyelesaian persamaan yang melibatkan akar pangkat tiga.
Pertanyaan 4: Di bidang apa saja akar pangkat tiga digunakan?
Akar pangkat tiga memiliki berbagai aplikasi dalam bidang-bidang seperti matematika, fisika, dan kimia. Dalam matematika, digunakan untuk menyelesaikan persamaan kubik. Dalam fisika, digunakan untuk menghitung volume benda beraturan dan persamaan gerak. Dalam kimia, digunakan untuk menghitung konsentrasi zat dalam larutan.
Kesimpulan:
Akar pangkat tiga adalah konsep matematika penting dengan beragam aplikasi. Memahami konsep dan sifatnya sangat penting untuk menyelesaikan masalah dan melakukan perhitungan di berbagai bidang.
Tips untuk Memahami Akar Pangkat Tiga:
Baca terus untuk mempelajari beberapa tips bermanfaat…
Tips Memahami Akar Pangkat Tiga
Dengan memahami tips berikut, Anda dapat meningkatkan pemahaman Anda tentang akar pangkat tiga:
Tip 1: Kuasai Definisi dan Notasi
Pahami konsep akar pangkat tiga sebagai kebalikan dari operasi pangkat tiga. Ketahui notasi penulisan akar pangkat tiga, yaitu simbol pangkat tiga ().
Tip 2: Latih Operasi Akar Pangkat Tiga
Kerjakan banyak soal latihan untuk memperkuat keterampilan menghitung akar pangkat tiga. Cobalah hitung secara manual dan menggunakan kalkulator untuk membandingkan hasilnya.
Tip 3: Pahami Sifat-sifat Akar Pangkat Tiga
Pelajari sifat-sifat akar pangkat tiga, seperti sifat asosiatif dan distributif. Sifat-sifat ini akan memudahkan Anda menyelesaikan persamaan yang melibatkan akar pangkat tiga.
Tip 4: Terapkan dalam Berbagai Bidang
Carilah contoh penerapan akar pangkat tiga dalam bidang matematika, fisika, dan kimia. Memahami aplikasi praktis akan memperkuat pemahaman Anda tentang konsep ini.
Dengan mengikuti tips ini secara konsisten, Anda dapat meningkatkan pemahaman Anda tentang akar pangkat tiga dan penggunaannya dalam berbagai bidang.
Kesimpulan
Akar pangkat tiga merupakan konsep matematika yang penting dan memiliki beragam aplikasi dalam berbagai bidang. Memahami akar pangkat tiga sangat penting untuk menyelesaikan masalah dan melakukan perhitungan di berbagai bidang, seperti matematika, fisika, dan kimia.
Artikel ini telah mengeksplorasi berbagai aspek akar pangkat tiga, termasuk definisi, notasi, sifat, metode hitung, sejarah, dan aplikasinya. Dengan memahami konsep dan sifat akar pangkat tiga, individu dapat menggunakannya secara efektif untuk menyelesaikan masalah dan memperoleh pemahaman yang lebih mendalam tentang konsep matematika.









