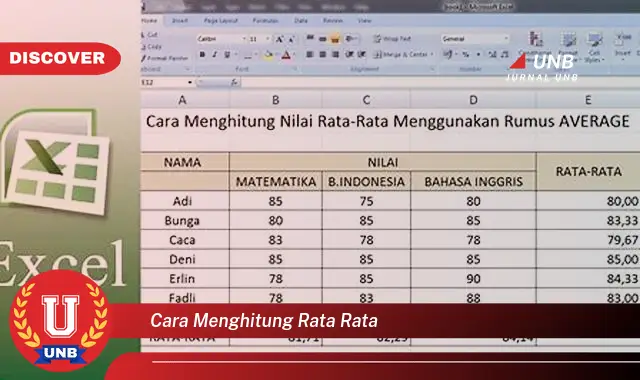
Cara menghitung rata-rata adalah metode untuk menemukan nilai rata-rata dari suatu kumpulan data. Rata-rata, juga dikenal sebagai mean, adalah ukuran tendensi sentral yang banyak digunakan dalam statistik dan matematika.
Cara menghitung rata-rata sangatlah penting karena memberikan informasi yang berharga tentang suatu kumpulan data. Rata-rata dapat digunakan untuk membandingkan kumpulan data yang berbeda, mengidentifikasi tren, dan membuat prediksi. Selain itu, rata-rata memiliki sejarah panjang dalam matematika dan statistik, sehingga menjadikannya konsep yang penting untuk dipahami.
Dalam artikel ini, kita akan membahas berbagai cara menghitung rata-rata, termasuk rata-rata aritmatika, rata-rata geometrik, dan rata-rata harmonik. Kita juga akan mengeksplorasi pentingnya rata-rata dan bagaimana rata-rata digunakan dalam berbagai bidang.
Cara Menghitung Rata-Rata
Cara menghitung rata-rata merupakan aspek penting dalam statistik dan matematika. Berikut adalah tujuh aspek penting yang terkait dengan cara menghitung rata-rata:
- Definisi
- Jenis-jenis rata-rata
- Rumus
- Aplikasi
- Kelebihan
- Kekurangan
- Contoh
Definisi rata-rata adalah nilai rata-rata dari suatu kumpulan data. Jenis-jenis rata-rata meliputi rata-rata aritmatika, rata-rata geometrik, dan rata-rata harmonik. Rumus untuk menghitung rata-rata aritmatika adalah jumlah semua data dibagi dengan jumlah data. Rata-rata memiliki banyak aplikasi, seperti dalam statistika deskriptif, inferensi statistik, dan analisis data.
Kelebihan rata-rata adalah mudah dihitung dan dipahami. Kekurangannya adalah rata-rata dapat dipengaruhi oleh nilai ekstrem (outlier). Contoh penggunaan rata-rata adalah untuk menghitung nilai rata-rata ujian siswa atau untuk menghitung pendapatan rata-rata suatu perusahaan.
Definisi
Definisi rata-rata sangat penting untuk memahami cara menghitung rata-rata. Rata-rata, juga dikenal sebagai mean, adalah ukuran tendensi sentral yang digunakan untuk mewakili nilai rata-rata dari suatu kumpulan data. Definisi ini memberikan dasar untuk mengembangkan rumus dan metode untuk menghitung rata-rata.
Tanpa definisi yang jelas, menghitung rata-rata akan menjadi tidak mungkin. Definisi memberikan kerangka kerja untuk menentukan apa yang dimaksud dengan “rata-rata” dan bagaimana cara mengukurnya. Ini juga memungkinkan kita untuk membandingkan kumpulan data yang berbeda dan membuat kesimpulan yang bermakna.
Sebagai contoh, jika kita ingin menghitung rata-rata nilai ujian siswa, kita perlu terlebih dahulu mendefinisikan apa yang dimaksud dengan “rata-rata”. Definisi rata-rata sebagai ukuran tendensi sentral memberi tahu kita bahwa kita perlu menjumlahkan semua nilai ujian dan membaginya dengan jumlah siswa. Definisi ini sangat penting untuk memastikan bahwa kita menghitung rata-rata dengan benar dan bahwa hasilnya bermakna.
Jenis-jenis Rata-rata
Jenis-jenis rata-rata merupakan komponen penting dalam memahami cara menghitung rata-rata. Terdapat tiga jenis rata-rata yang umum digunakan, yaitu rata-rata aritmatika, rata-rata geometrik, dan rata-rata harmonik. Masing-masing jenis rata-rata memiliki rumus dan aplikasi yang berbeda, tergantung pada jenis data dan tujuan perhitungan.
Rata-rata aritmatika, yang juga dikenal sebagai mean, adalah jenis rata-rata yang paling umum digunakan. Rata-rata aritmatika dihitung dengan menjumlahkan semua nilai data dan membaginya dengan jumlah data. Rata-rata aritmatika sangat cocok digunakan untuk data yang berdistribusi normal atau simetris.
Rata-rata geometrik digunakan untuk menghitung rata-rata dari data yang berdistribusi miring atau tidak simetris. Rata-rata geometrik dihitung dengan mengalikan semua nilai data dan kemudian mengambil akar pangkat jumlah data. Rata-rata geometrik sangat cocok digunakan untuk data yang menunjukkan pertumbuhan atau penurunan secara eksponensial.
Rata-rata harmonik digunakan untuk menghitung rata-rata dari data yang memiliki nilai nol. Rata-rata harmonik dihitung dengan menjumlahkan kebalikan dari semua nilai data dan kemudian membagi dengan jumlah data. Rata-rata harmonik sangat cocok digunakan untuk data yang menunjukkan kecepatan atau tingkat.
Memahami jenis-jenis rata-rata sangat penting untuk memilih metode perhitungan rata-rata yang tepat. Pemilihan jenis rata-rata yang tepat akan menghasilkan hasil yang lebih akurat dan bermakna.
Rumus
Rumus merupakan komponen penting dalam cara menghitung rata-rata. Rumus menyediakan langkah-langkah yang jelas dan sistematis untuk menghitung rata-rata dari suatu kumpulan data. Tanpa rumus, menghitung rata-rata akan menjadi proses yang sulit dan tidak akurat.
-
Jenis-jenis Rumus
Terdapat tiga jenis rumus rata-rata yang umum digunakan, yaitu rumus rata-rata aritmatika, rumus rata-rata geometrik, dan rumus rata-rata harmonik. Masing-masing jenis rumus memiliki fungsi dan aplikasi yang berbeda, tergantung pada jenis data dan tujuan perhitungan.
-
Aplikasi Rumus
Rumus rata-rata memiliki banyak aplikasi dalam kehidupan sehari-hari. Beberapa contoh aplikasi rumus rata-rata antara lain menghitung nilai rata-rata ujian siswa, menghitung pendapatan rata-rata suatu perusahaan, dan menghitung kecepatan rata-rata suatu kendaraan.
-
Kelebihan Rumus
Rumus rata-rata memiliki beberapa kelebihan, antara lain mudah dipahami dan diterapkan, memberikan hasil yang akurat, dan dapat digunakan untuk menghitung rata-rata dari berbagai jenis data.
-
Kekurangan Rumus
Selain kelebihan, rumus rata-rata juga memiliki beberapa kekurangan. Salah satu kekurangannya adalah rumus rata-rata dapat dipengaruhi oleh nilai ekstrem (outlier). Selain itu, rumus rata-rata tidak selalu cocok digunakan untuk data yang berdistribusi tidak normal.
Memahami rumus rata-rata sangat penting untuk menghitung rata-rata secara akurat dan efisien. Dengan memahami rumus rata-rata, kita dapat memperoleh informasi yang berharga dari suatu kumpulan data dan membuat keputusan yang lebih baik.
Aplikasi
Aplikasi merupakan salah satu komponen penting dalam memahami cara menghitung rata-rata. Aplikasi merujuk pada penggunaan rumus dan metode rata-rata dalam berbagai bidang kehidupan nyata. Memahami aplikasi rata-rata sangat penting karena memberikan konteks dan tujuan praktis dari perhitungan rata-rata.
Salah satu contoh aplikasi rata-rata yang paling umum adalah dalam bidang statistik. Rata-rata digunakan untuk meringkas dan menganalisis data, seperti menghitung nilai rata-rata ujian siswa atau menghitung pendapatan rata-rata suatu perusahaan. Rata-rata juga digunakan dalam bidang keuangan, seperti menghitung suku bunga rata-rata atau menghitung pengembalian investasi rata-rata.
Selain itu, rata-rata juga memiliki aplikasi dalam bidang sains dan teknik. Misalnya, rata-rata digunakan untuk menghitung kecepatan rata-rata suatu kendaraan atau menghitung suhu rata-rata suatu ruangan. Rata-rata juga digunakan dalam bidang manufaktur, seperti menghitung waktu produksi rata-rata atau menghitung tingkat cacat rata-rata.
Memahami aplikasi rata-rata sangat penting untuk mengapresiasi pentingnya dan kegunaan rata-rata dalam berbagai bidang. Dengan memahami aplikasi rata-rata, kita dapat menggunakan rata-rata secara efektif untuk memperoleh informasi yang berharga dari data dan membuat keputusan yang lebih baik.
Kelebihan
Kelebihan merupakan salah satu komponen penting dalam memahami cara menghitung rata-rata. Kelebihan merujuk pada keunggulan dan manfaat yang dimiliki oleh cara menghitung rata-rata, menjadikannya metode yang efektif dan efisien untuk meringkas dan menganalisis data.
Salah satu kelebihan utama cara menghitung rata-rata adalah kemudahannya. Rumus rata-rata mudah dipahami dan diterapkan, sehingga dapat digunakan oleh siapa saja tanpa memerlukan pengetahuan matematika yang mendalam. Selain itu, cara menghitung rata-rata dapat diaplikasikan pada berbagai jenis data, sehingga sangat fleksibel dan serbaguna.
Kelebihan lainnya dari cara menghitung rata-rata adalah akurasinya. Rata-rata memberikan representasi yang akurat dari nilai rata-rata suatu kumpulan data, sehingga dapat digunakan sebagai dasar untuk membuat keputusan dan kesimpulan yang tepat. Rata-rata juga dapat digunakan untuk membandingkan kumpulan data yang berbeda dan mengidentifikasi tren dan pola.
Memahami kelebihan cara menghitung rata-rata sangat penting untuk mengapresiasi keunggulan dan manfaat metode ini. Dengan memahami kelebihan rata-rata, kita dapat menggunakannya secara efektif untuk memperoleh informasi yang berharga dari data dan membuat keputusan yang lebih baik.
Kekurangan
Dalam konteks cara menghitung rata-rata, terdapat beberapa kekurangan yang perlu diperhatikan. Kekurangan-kekurangan ini dapat memengaruhi keakuratan dan keandalan rata-rata sebagai ukuran tendensi sentral.
-
Pengaruh Nilai Ekstrem
Salah satu kekurangan cara menghitung rata-rata adalah pengaruhnya terhadap nilai ekstrem. Nilai ekstrem adalah nilai data yang jauh lebih besar atau lebih kecil dari nilai lainnya dalam kumpulan data. Keberadaan nilai ekstrem dapat mendistorsi nilai rata-rata, sehingga tidak lagi mewakili nilai rata-rata sebenarnya dari kumpulan data.
-
Ketidaksesuaian untuk Data Non-Normal
Cara menghitung rata-rata mengasumsikan bahwa data berdistribusi normal atau simetris. Namun, dalam praktiknya, banyak kumpulan data yang tidak berdistribusi normal. Ketika data tidak berdistribusi normal, rata-rata mungkin bukan ukuran tendensi sentral yang paling tepat.
-
Kepekaan terhadap Perubahan Data
Rata-rata sangat sensitif terhadap perubahan data. Penambahan atau penghapusan bahkan satu nilai data dapat secara signifikan mengubah nilai rata-rata. Hal ini dapat menjadi masalah ketika data tidak lengkap atau tidak akurat.
Memahami kekurangan cara menghitung rata-rata sangat penting untuk menggunakannya secara efektif. Dengan menyadari keterbatasannya, kita dapat mengambil langkah-langkah untuk meminimalkan pengaruh kekurangan tersebut dan memastikan bahwa rata-rata memberikan representasi yang akurat dari kumpulan data.
Contoh
Contoh sangat penting dalam memahami cara menghitung rata-rata. Contoh memberikan ilustrasi praktis tentang bagaimana rata-rata dihitung dan digunakan dalam berbagai situasi kehidupan nyata.
-
Contoh 1: Menghitung Nilai Rata-Rata Ujian
Seorang guru ingin menghitung nilai rata-rata ujian matematika untuk kelasnya. Guru tersebut menjumlahkan nilai semua siswa dan membaginya dengan jumlah siswa. Nilai rata-rata yang diperoleh dapat digunakan untuk mengukur kinerja kelas secara keseluruhan.
-
Contoh 2: Menghitung Pendapatan Rata-Rata Perusahaan
Sebuah perusahaan ingin menghitung pendapatan rata-rata per bulan selama setahun. Perusahaan tersebut menjumlahkan pendapatan setiap bulan dan membaginya dengan jumlah bulan. Pendapatan rata-rata yang diperoleh dapat digunakan untuk menganalisis kinerja keuangan perusahaan.
-
Contoh 3: Menghitung Kecepatan Rata-Rata Mobil
Seorang pengemudi ingin menghitung kecepatan rata-rata mobilnya selama perjalanan. Pengemudi tersebut mencatat waktu tempuh dan jarak tempuh. Kecepatan rata-rata dapat dihitung dengan membagi jarak tempuh dengan waktu tempuh. Kecepatan rata-rata yang diperoleh dapat digunakan untuk mengukur efisiensi bahan bakar mobil.
Contoh-contoh ini menunjukkan bagaimana cara menghitung rata-rata dapat diterapkan dalam berbagai situasi untuk memperoleh informasi yang berharga dan membuat keputusan yang lebih baik.
Pertanyaan yang Sering Diajukan (FAQ)
Bagian FAQ ini memberikan jawaban atas beberapa pertanyaan umum terkait cara menghitung rata-rata. Pemahaman yang jelas tentang konsep rata-rata sangat penting untuk menganalisis data secara akurat dan efektif.
Pertanyaan 1: Apa itu rata-rata?
Rata-rata, juga dikenal sebagai mean, adalah ukuran tendensi sentral yang mewakili nilai rata-rata dari suatu kumpulan data. Rata-rata digunakan untuk meringkas dan membandingkan kumpulan data yang berbeda.
Pertanyaan 2: Kapan sebaiknya menggunakan rata-rata?
Rata-rata sangat cocok digunakan ketika data berdistribusi normal atau simetris. Rata-rata juga dapat digunakan untuk membandingkan kumpulan data yang berbeda, mengidentifikasi tren, dan membuat prediksi.
Pertanyaan 3: Apa saja kekurangan rata-rata?
Rata-rata dapat dipengaruhi oleh nilai ekstrem (outlier) dan tidak selalu cocok digunakan untuk data yang berdistribusi tidak normal. Selain itu, rata-rata dapat sensitif terhadap perubahan data.
Pertanyaan 4: Bagaimana cara menghitung rata-rata?
Rumus untuk menghitung rata-rata adalah jumlah semua nilai data dibagi dengan jumlah data. Terdapat juga jenis rata-rata lainnya, seperti rata-rata geometrik dan rata-rata harmonik, yang digunakan untuk tujuan tertentu.
Kesimpulan:
Pemahaman tentang cara menghitung rata-rata sangat penting untuk menganalisis data secara akurat dan efektif. Dengan memahami konsep rata-rata dan keterbatasannya, kita dapat menggunakan rata-rata dengan tepat untuk memperoleh informasi yang berharga dan membuat keputusan yang lebih baik.
Tips:
Untuk mempelajari lebih lanjut tentang cara menghitung rata-rata, silakan baca artikel Tips berikut ini…
Tips Menghitung Rata-Rata
Menghitung rata-rata merupakan keterampilan penting dalam statistik dan analisis data. Berikut adalah beberapa tips untuk membantu Anda menghitung rata-rata secara akurat dan efisien:
Tip 1: Tentukan Jenis Rata-Rata
Terdapat tiga jenis rata-rata yang umum digunakan: rata-rata aritmatika, rata-rata geometrik, dan rata-rata harmonik. Pilih jenis rata-rata yang sesuai dengan jenis data dan tujuan perhitungan.
Tip 2: Periksa Nilai Ekstrem
Nilai ekstrem (outlier) dapat memengaruhi nilai rata-rata. Periksa kumpulan data untuk adanya nilai ekstrem dan pertimbangkan untuk mengecualikannya dari perhitungan jika perlu.
Tip 3: Gunakan Kalkulator atau Perangkat Lunak
Untuk kumpulan data yang besar, gunakan kalkulator atau perangkat lunak untuk menghitung rata-rata. Hal ini dapat membantu meminimalkan kesalahan perhitungan.
Tip 4: Verifikasi Hasil
Setelah menghitung rata-rata, verifikasi hasilnya dengan menghitung ulang atau menggunakan metode alternatif. Hal ini memastikan bahwa rata-rata yang diperoleh akurat.
Dengan mengikuti tips ini, Anda dapat menghitung rata-rata secara akurat dan efisien, sehingga memperoleh informasi yang lebih bermakna dari kumpulan data Anda.
Kesimpulan
Pemahaman yang baik tentang cara menghitung rata-rata sangat penting dalam menganalisis dan menginterpretasikan data. Rata-rata memberikan ukuran tendensi sentral yang dapat digunakan untuk membandingkan kumpulan data yang berbeda, mengidentifikasi tren, dan membuat prediksi.
Dengan memahami konsep rata-rata, jenis-jenis rata-rata, dan keterbatasannya, kita dapat menggunakan rata-rata secara efektif untuk memperoleh informasi yang berharga dan membuat keputusan yang lebih baik. Rata-rata akan terus menjadi alat yang penting dalam berbagai bidang, termasuk statistik, keuangan, sains, dan teknik.









